Tổng hợp các công thức con lắc đơn và các dạng bài tập về con lắc đơn.

Khái niệm về con lắc đơn

Con lắc đơn gồm một vật nhỏ, khối lượng m, treo ở đầu của một sợi dây không dãn, khối lượng không đáng kể, dài l

Dao động điều hòa của con lắc đơn

Phương trình dao động điều hòa của con lắc đơn:

$s = {s_0}{\rm{cos(}}\omega {\rm{t + }}\varphi {\rm{) hay }}\alpha {\rm{ = }}{\alpha _0}{\rm{cos(}}\omega {\rm{t + }}\varphi {\rm{)}}$ với ${s_0} = l{\alpha _0}$

Các đại lượng trong dao động điều hòa của con lắc đơn:

Tần số góc, chu kì, tần số:
$\omega = \sqrt {\frac{g}{l}} ,{\rm{ }}T = 2\pi \sqrt {\frac{l}{g}}$

Điều kiện để con lắc đơn dao động điều hòa: dao động nhỏ ( $\sin \alpha \approx \alpha$ )
Hệ thức độc lập: $s_0^2 = {s^2} + \frac{{{v^2}}}{{{\omega ^2}}}$ hay $\alpha _0^2 = {\alpha ^2} + \frac{{{v^2}}}{{{l^2}{\omega ^2}}}$ hoặc $\alpha _0^2 = {\alpha ^2} + \frac{{{v^2}}}{{lg}}$

Năng lượng của con lắc đơn

Động năng: ${W_d} = \frac{1}{2}m{v^2}$

Thế năng: ${W_t} = mgl(1 - c{\rm{os}}\alpha {\rm{)}}$

Cơ năng – ĐL bảo toàn cơ năng:
$W = {W_d} + {W_t} = \frac{1}{2}m{v^2} + {W_t} \\= mgl(1 - c{\rm{os}}\alpha {\rm{) = h/s}}$

Các dạng bài tập về con lắc đơn

Dạng 1: Xác định các đại lượng cơ bản trong dao động điều hòa của con lắc đơn

– Tìm $\omega ,{\rm{ }}{\bf{T}},{\rm{ }}{\bf{f}}$ : Đề cho l, g:

$\omega = \sqrt {\frac{g}{l}} ,T = \frac{{2\pi }}{\omega } = 2\pi \sqrt {\frac{l}{g}} ,f = \frac{\omega }{{2\pi }} = \frac{1}{{2\pi }}\sqrt {\frac{g}{l}}$

– Tìm gia tốc rơi tự do:

$T = \frac{{2\pi }}{\omega } = 2\pi \sqrt {\frac{l}{g}} \to g = \frac{{4{\pi ^2}l}}{{{T^2}}}$

Dạng 2: Tìm $\omega ,{\rm{ }}{\bf{T}},{\rm{ }}{\bf{f}}$ : thay đổi chiều dài dây treo l

Trong cùng khoảng thời gian t, hai con lắc thực hiện N1 và N2 dao động:
$f = \frac{N}{t} \to \frac{g}{l} = {\omega ^2} = {(2\pi f)^2} = {(\frac{{2\pi N}}{t})^2} \\\to \frac{{{l_2}}}{{{l_1}}} = {(\frac{{{N_1}}}{{{N_2}}})^2}$

Thay đổi chiều dài con lắc:
Ta có: ${T^2} \sim l,{f^2} \sim \frac{1}{l},{\omega ^2} \sim \frac{1}{l}$

Ta suy ra:

${(\frac{{{\omega _1}}}{{{\omega _2}}})^2} = {(\frac{{{f_1}}}{{{f_2}}})^2} = \frac{{{l_2}}}{{{l_1}}} = \frac{{{l_1} \pm \Delta l}}{{{l_1}}}$

Ta có: ${T_1} = 2\pi \sqrt {\frac{{{\ell _1}}}{g}} \Rightarrow {\rm{T}}_1^2 = 4{\pi ^2}.\frac{{{\ell _1}}}{g};{T_2} = 2\pi \sqrt {\frac{{{\ell _2}}}{g}} \\\Rightarrow {\rm{T}}_2^2 = 4{\pi ^2}.\frac{{{\ell _2}}}{g}$

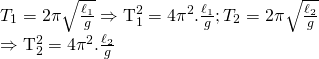
Chu kỳ của con lắc có chiều dài ${\ell _3} = {\ell _1} \pm {\ell _2}$ là: ${T_3} = 2\pi \sqrt {\frac{{{\ell _1} + {\ell _2}}}{g}} \\\Rightarrow T_3^2 = 4{\pi ^2}.\left( {\frac{{{\ell _1} \pm {\ell _2}}}{g}} \right) = T_1^2 \pm T_2^2$

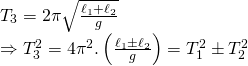
Dạng 3: Viết phương trình dao động điều hòa của con lắc đơn

Bước 1: Xác định biên độ góc: ${S_0},{\alpha _0}.$
Sử dụng các dữ kiện đầu bài cho và hệ thức độc lập với thời gian: $s_0^2 = {s^2} + \frac{{{v^2}}}{{{\omega ^2}}}$ hay $\alpha _0^2 = {\alpha ^2} + \frac{{{v^2}}}{{{l^2}{\omega ^2}}}$ hoặc $\alpha _0^2 = {\alpha ^2} + \frac{{{v^2}}}{{lg}}$

Bước 2: Xác định tần số góc ω: $\omega = \sqrt {\frac{g}{l}} = \frac{{2\pi }}{T} = 2\pi f$

Bước 3: Xác định pha ban đầu: $\varphi$
Tại $t{\rm{ }} = {\rm{ }}0:\left\{ \begin{array}{l}s = {s_0}{\rm{cos}}\varphi \\v = - \omega {s_0}\sin \varphi \end{array} \right.$

Bước 4: Viết PTDĐ: $s = {s_0}{\rm{cos(}}\omega {\rm{t + }}\varphi {\rm{) hay }}\alpha {\rm{ = }}{\alpha _0}{\rm{cos(}}\omega {\rm{t + }}\varphi {\rm{)}}$
Với ${s_0} = l{\alpha _0}$
Sotayhoctap chúc các bạn học tốt!