Bài viết góc giữa đường thẳng và mặt phẳng bao gồm: góc giữa đường thẳng và mặt phẳng oxyz, cách xác định góc giữa đường thẳng và mặt phẳng, công thức tính góc giữa đường thẳng và mặt phẳng, bài tập tính góc giữa đường thẳng và mặt phẳng…
Góc giữa đường thẳng và mặt phẳng oxyz
Cho đường thẳng ![]() có 1 VTCP
có 1 VTCP ![]()

(P) có 1 VTPT ![]()
![]()
![]() không vuông góc với (P)
không vuông góc với (P)
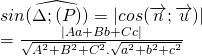
Cách xác định góc giữa đường thẳng và mặt phẳng
Để xác định góc giữa đường thẳng a và mặt phẳng αta thực hiện theo các bước sau:

- Tìm giao điểm

- Dựng hình chiếu A’ của một điểm
 xuống α
xuống α - Góc
 chính là góc giữa đường thẳng a và α.
chính là góc giữa đường thẳng a và α.
Lưu ý:
Để dựng hình chiếu A’ của điểm A trên α ta chọn một đường thẳng ![]() khi đó
khi đó ![]() .
.
Để tính góc ![]() ta sử dung hệ thức lượng trong tam giác vuông
ta sử dung hệ thức lượng trong tam giác vuông ![]() . Ngoài ra nếu không xác định góc
. Ngoài ra nếu không xác định góc ![]() thì ta có thể tính góc giữa đường thẳng a và mặt phẳng α theo công thức
thì ta có thể tính góc giữa đường thẳng a và mặt phẳng α theo công thức ![]() trong đó
trong đó ![]() là VTCP của a còn
là VTCP của a còn ![]() là vec tơ có giá vuông góc với α.
là vec tơ có giá vuông góc với α.
Ví dụ bài tập tính góc giữa đường thẳng và mặt phẳng
Ví dụ 1: Cho tam giác ABC vuông cân tại A và BC = a. Trên đường thẳng qua A vuông góc với (ABC) lấy điểm S sao cho SA=a6√2. Tính số đo góc giữa đường thẳng SA và (ABC).
Lời giải:

![]() .
.
Ví dụ 2: Cho ![]() và
và ![]() . Tính góc giữa
. Tính góc giữa ![]() và (P)
và (P)
Lời giải:
![]() có 1 VTCP
có 1 VTCP ![]()
(P) có 1 VTCP ![]()
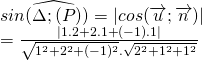
![]()
![]()
Ví dụ 3: Cho 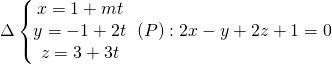 . Tìm m để
. Tìm m để ![]()
Lời giải:
![]() có 1 VTCP
có 1 VTCP ![]()
(P) có 1 VTCP ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Ví dụ 4: Cho đường thẳng d1 là giao tuyến của hai mặt phẳng ![]() . Viết phương trình (P) chứ d1 và tạo
. Viết phương trình (P) chứ d1 và tạo ![]() một góc 600
một góc 600
Lời giải:
(P) chứa giao tuyến 2 mặt phẳng ![]() nên có phương trình
nên có phương trình
![]()
![]()
(P) có 1 VTCP ![]()
d2 có 1 VTCP ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
TH1:
![]()
TH2:
m = -n chọn m = 1, n = -1
pt (P): x – z = 0
KL:
x +y – 2 = 0
x – z = 0
Sotayhoctap chúc các bạn học tốt!




