Bảng nguyên hàm: Nguyên hàm của các hàm số sơ cấp, nguyên hàm của hàm số hợp…

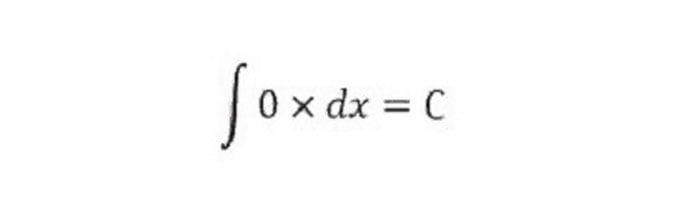
Nguyên hàm là gì?

Hàm số $F_{(x)}$ được gọi là nguyên hàm của hàm số $f_{(x)}$ trên (a;b) nếu $F'_{(x)} = f_{(x)}$

Ví dụ:

Hàm số $y = x^{2}$ là nguyên hàm của hàm số $y = 2x$ trên $\mathbb{R}$ vì $(x^{2})' = 2x$

Hàm số $y = \ln x$ là nguyên hàm của hàm số $y = \frac{1}{x}$ trên $(0,+\infty )$ vì $(\ln x)' = \frac{1}{x}$

Tính chất của nguyên hàm

$(\int f_{(x)}dx)' = f_{x}$
$\int a.f_{(x)}dx = a.\int f_{(x)}dx$
$\int \left [ f_{(x)} \pm g_{(x)} \right ]dx = \int f_{(x)}dx \pm \int g_{(x)}dx$

Bảng nguyên hàm đầy đủ của hàm số cơ bản

	Nguyên hàm của các hàm số sơ cấp	Nguyên hàm của các hàm số hợp u = u(x)
Lũy thừa	$\int dx = x + C$	$\int du = u + C$
Lũy thừa	$\int x^{a }dx = \frac{x^{a + 1}}{a + 1} + C$	$\int u^{a }dx = \frac{u^{a + 1}}{a + 1} + C$
Mũ logarit	$\int {\frac{{dx}}{x} = \ln \left\| x \right\| + C} \,\,\left( {x \ne 0} \right)$	$\int {\frac{{du}}{u} = \ln \left\| u \right\| + C} \,\,\left( {x \ne 0} \right)$
	$\int {{e^x}dx = {e^x} + C}$	$\int {{e^u}dx = {e^u} + C}$
	$\int {{a^x}dx = \frac{{{a^x}}}{{\ln a}} + C\,\,\left( {0 < a \ne 1} \right)}$	$\int {{a^u}du = \frac{{{a^u}}}{{\ln a}} + C\,\,\left( {0 < a \ne 1} \right)}$
Lượng giác	$\int {\cos xdx = \sin x + C}$	$\int {\cos udu = \sin u + C}$
	$\int {\sin xdx = - \cos x + C}$	$\int {\sin udu = - \cos u + C}$
	$\int {\frac{{dx}}{{\sin x}}} = \ln \left\| {\tan \frac{x}{2}} \right\| + C$	$\int {\frac{{du}}{{\sin u}}} = \ln \left\| {\tan \frac{u}{2}} \right\| + C$
	$\int {\frac{{dx}}{{\cos x}}} = \ln \left\| {\tan \left( {\frac{x}{2} + \frac{\pi }{4}} \right)} \right\| + C$	$\int {\frac{{du}}{{\cos u}}} = \ln \left\| {\tan \left( {\frac{u}{2} + \frac{\pi }{4}} \right)} \right\| + C$
	$\int {\frac{{dx}}{{{{\cos }^2}x}} = \tan x + C}$	$\int {\frac{{du}}{{{{\cos }^2}u}} = \tan u + C}$
	$\int {\frac{{dx}}{{{{\sin }^2}x}} = - \cot x + C}$	$\int {\frac{{du}}{{{{\sin }^2}u}} = - \cot u + C}$
	$\int \cot xdx = \ln \left \| sinx \right \| + C$	$\int \cot udu = \ln \left \| sinu \right \| + C$
	$\int \tan xdx = -\ln \left \| \cos x \right \| + C$	$\int \tan udu = -\ln \left \| \cos u \right \| + C$
Căn thức	$\int \frac{dx}{\sqrt{x}} = 2\sqrt{x} + C$	$\int \frac{du}{\sqrt{u}} = 2\sqrt{u} + C$
	$\int \sqrt[n]{x}dx = \frac{n}{n+1}\sqrt[n]{x^{n+1}} + C$	$\int \sqrt[n]{u}du = \frac{n}{n+1}\sqrt[n]{u^{n+1}} + C$
	$\int \frac{dx}{\sqrt{x^{2}\pm a}} = \ln \left \| x + \sqrt{x^{2}\pm a} \right \| + C$	$\int \frac{du}{\sqrt{u^{2}\pm a}} = \ln \left \| u + \sqrt{u^{2}\pm a} \right \| + C$
	$\int \frac{dx}{\sqrt{a^{2} - x^{2}}} = \arcsin \frac{x}{a} + C$	$\int \frac{du}{\sqrt{a^{2} - u^{2}}} = \arcsin \frac{u}{a} + C$
	$\int {\frac{{xdx}}{{\sqrt {{x^2} \pm {a^2}} }}} = \sqrt {{x^2} \pm {a^2}} + C$	$\int {\frac{{udu}}{{\sqrt {{u^2} \pm {a^2}} }}} = \sqrt {{u^2} \pm {a^2}} + C$
	$\int {\sqrt {{x^2} \pm {a^2}} } dx = \frac{x}{2}\sqrt {{x^2} + {a^2}} \pm \frac{a}{2}\ln \left\| {x + \sqrt {{x^2} \pm {a^2}} } \right\| + C$	$\int {\sqrt {{u^2} \pm {a^2}} } du = \frac{u}{2}\sqrt {{u^2} + {a^2}} \pm \frac{a}{2}\ln \left\| {u + \sqrt {{u^2} \pm {a^2}} } \right\| + C$
Phân thức hữu tỷ	$\int \frac{dx}{x^{2}} = -\frac{1}{x} + C$	$\int \frac{du}{u^{2}} = -\frac{1}{u} + C$
	$\int \frac{dx}{x^{n}} = \frac{-1}{(n - 1)x^{n - 1}} + C$	$\int \frac{du}{u^{n}} = \frac{-1}{(n - 1)u^{n - 1}} + C$
	$\int \frac{dx}{x^{2} - a^{2}} = \frac{1}{2a}\ln \left \| \frac{x - a}{x + a} \right \| + C$	$\int \frac{du}{u^{2} - a^{2}} = \frac{1}{2a}\ln \left \| \frac{u - a}{u + a} \right \| + C$
	$\int \frac{dx}{x^{2} + a^{2}} = \frac{1}{a}\arctan \frac{x}{a} + C$	$\int \frac{du}{u^{2} + a^{2}} = \frac{1}{a}\arctan \frac{u}{a} + C$
	$\int {\frac{{xdx}}{{{x^2} \pm {a^2}}}} = \frac{1}{2}\ln \left\| {{x^2} \pm {a^2}} \right\| + C$	$\int {\frac{{udu}}{{{u^2} \pm {a^2}}}} = \frac{1}{2}\ln \left\| {{u^2} \pm {a^2}} \right\| + C$