Công thức tích phân: Công thức tích phân cơ bản, công thức tích phân từng phần, tính chất của tích phân, ứng dụng của tích phân…
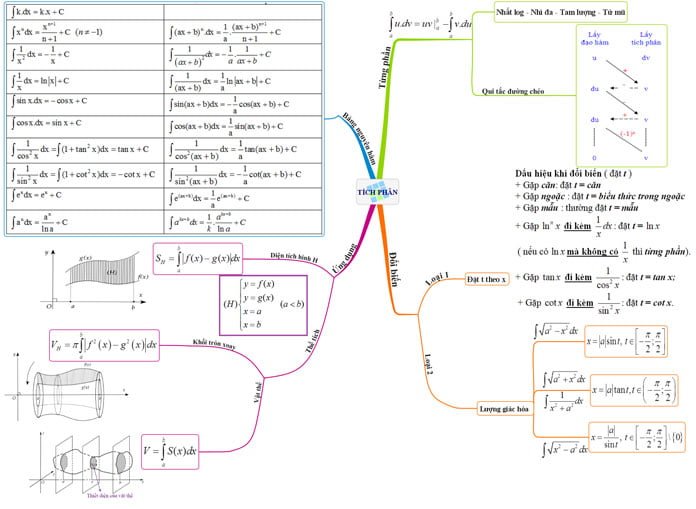
Định nghĩa tích phân
Cho hàm ![]() liên tục trên khoảng K và a, b là hai số bất kỳ thuộc K. Nếu
liên tục trên khoảng K và a, b là hai số bất kỳ thuộc K. Nếu ![]() là một nguyên hàm của
là một nguyên hàm của ![]() thì hiệu số
thì hiệu số ![]() được gọi là tích phân của
được gọi là tích phân của ![]() từ a đến b và ký hiệu là
từ a đến b và ký hiệu là ![]()
Tính chất của tích phân – Công thức tích phân
Cho các hàm số ![]() liên tục trên K và
liên tục trên K và ![]() là ba số thuộc K.
là ba số thuộc K.
![]()
![]()
![]()
![]()
![]()
Một số phương pháp tính tích phân
Phương pháp đổi biến số
Công thức đổi biến số ![Rendered by QuickLaTeX.com \int\limits_a^b {f[u(x)]u'(x)dx = \int\limits_{u(a)}^{u(b)} {f(u)du} }.](https://sotayhoctap.com/wp-content/ql-cache/quicklatex.com-d7ecb3efc65ab4102c5fa6802bbbeaa9_l3.png) Trong đó
Trong đó ![]() là hàm số liên tục và
là hàm số liên tục và ![]() có đạo hàm liên tục trên khoảng J sao cho hàm hợp
có đạo hàm liên tục trên khoảng J sao cho hàm hợp ![]() xác định trên J;
xác định trên J; ![]()
Các phương pháp đổi biến số thường gặp:
Cách 1: Đặt ![]() (
(![]() là một hàm theo
là một hàm theo ![]() ).
).
Cách 2: Đặt ![]() (
(![]() là một hàm theo
là một hàm theo ![]() ).
).
Phương pháp tích phân từng phần
Định lí:
Nếu ![]() là hai hàm số có đạo hàm liên tục trên khoảng K và
là hai hàm số có đạo hàm liên tục trên khoảng K và ![]() là hai số thuộc K thì
là hai số thuộc K thì ![]()
Bài tập minh họa áp dụng công thức tích phân
Ví dụ 1:
Áp dụng công thức tính tích phân cơ bản, tính các tích phân sau:
a) ![]()
b) ![]()
Lời giải:
a) ![]()
![]()
b) ![]()
Ví dụ 2:
Áp dụng phương pháp đổi biến số, tính các tích phân sau:
a) ![]()
b) ![]()
c) ![]()
Lời giải:
a) Đặt: ![]()
Đổi cận ![]()
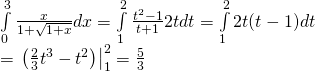
b) Đặt: ![]()
Đổi cận: ![]()
Vậy: ![]()
c) Đặt ![]() với
với ![]()
Đổi cận: ![]()
Vậy: ![]()
Ví dụ 3:
Vận dụng phương pháp tính tích phân từng phân, tính các tích phân sau:
a) ![]()
b) ![]()
Lời giải:
a) Đặt: ![]()
![]() .
.
b) Đặt: ![]()
![]()
![]() .
.
Sotayhoctap chúc các bạn học tốt!




