Chuyên đề số chính phương: số chính phương là số gì, định nghĩa số chính phương, tính chất số chính phương, một số dạng bài tập về số chính phương…

Số chính phương

Số chính phương là số gì?

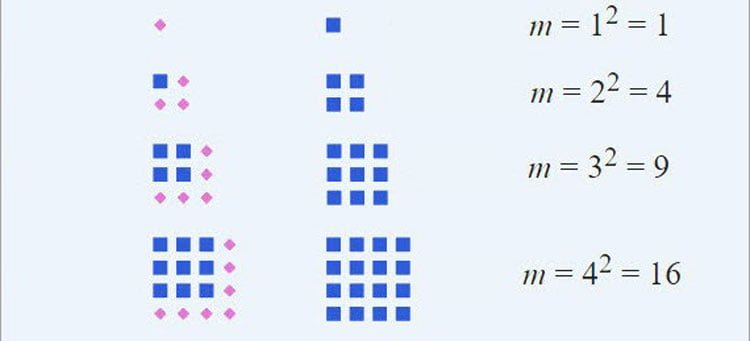
Số chính phương hay còn gọi là số hình vuông là số tự nhiên có căn bậc 2 là một số tự nhiên, hay nói cách khác, số chính phương là bình phương (lũy thừa bậc 2) của một số tự nhiên. Số chính phương hiển thị diện tích của một hình vuông có chiều dài cạnh bằng số nguyên kia.

Định nghĩa số chính phương

Số chính phương là số bằng bình phương đúng của một số nguyên.

Tính chất số chính phương

– Số chính phương chỉ có thể có chữ số tận cùng bằng 0, 1, 4, 5, 6, 9; không thể có chữ tận cùng bằng 2, 3, 7, 8.

– Khi phân tích ra thừa số nguyên tố, số chính phương chỉ chứa các thừa số nguyên tố với số mũ chẵn.

– Số chính phương chỉ có thể có một trong hai dạng 4n hoặc 4n + 1. Không có số chính phương nào có dạng 4n + 2 hoặc 4n + 3 (n ∈ N).

– Số chính phương chỉ có thể có một trong hai dạng 3n hoặc 3n + 1. Không có số chính phương nào có dạng 3n + 2 (n ∈ N).

– Số chính phương tận cùng bằng 1, 4 hoặc 9 thì chữ số hàng chục là chữ số chẵn.

+ Số chính phương tận cùng bằng 5 thì chữ số hàng chục là 2.

+ Số chính phương tận cùng bằng 6 thì chữ số hàng chục là chữ số lẻ.

– Số chính phương chia hết cho 2 thì chia hết cho 4.

+ Số chính phương chia hết cho 3 thì chia hết cho 9

+ Số chính phương chia hết cho 5 thì chia hết cho 25

+ Số chính phương chia hết cho 8 thì chia hết cho 16.

Một số dạng bài tập về số chính phương

Dạng 1: Chứng minh một số là số chính phương

Ví dụ 1: Chứng minh rằng mọi số nguyên x, y thì:

A = (x + y)(x + 2y)(x + 3y)(x + 4y) + là số chính phương.

Giải: Ta có A = (x + y)(x + 2y)(x + 3y)(x + 4y) + y4

= (x² + 5xy + 4y²)(x² + 5xy + 6y²) + y⁴

Đặt x² + 5xy + 5y² = t (t Z) thì

A = (t – y²)(t + y²) + y⁴ = t² – y⁴ + y⁴ = t2 = (x² + 5xy + 5y²)²

Vì x, y, z Z nên x² Z, 5xy Z, 5y² Z => (x² + 5xy + 5y²) Z

Vậy A là số chính phương.

Ví dụ 2: Chứng minh tích của 4 số tự nhiên liên tiếp cộng 1 luôn là số chính phương.

Giải: Gọi 4 số tự nhiên, liên tiếp đó là n, n + 1, n + 2, n + 3 (n ∈ Z). Ta có:

n(n + 1)(n + 2)(n + 3) + 1 = n . ( n + 3)(n + 1)(n + 2) + 1

= (n² + 3n)(n² + 3n + 2) + 1 (*)

Đặt n² + 3n = t (t N) thì (*) = t(t + 2) + 1 = t² + 2t + 1 = (t + 1)²

= (n² + 3n + 1)²

Vì n N nên n2 + 3n + 1 N. Vậy n(n + 1)(n + 2)(+ 3) + 1 là số chính phương.

Dạng 2: Tìm giá trị của biến để biểu thức là số chính phương

Ví dụ: Tìm số tự nhiên n sao cho các số sau là số chính phương:

n² + 2n + 12

Giải:

Vì n² + 2n + 12 là số chính phương nên đặt n² + 2n + 12 = k² (k N)

=> (n² + 2n + 1) + 11 = k² <=> k² – (n+1)² = 11 <=> (k + n + 1).(k – n – 1) = 11

Nhận xét thấy k + n + 1 > k – n – 1 và chúng là các số nguyên dương, nên ta có thể viết:

Dạng 3: tìm số chính phương

Ví dụ: Tìm một số chính phương gồm 4 chữ số biết rằng số gồm 2 chữ số đầu lớn hơn số gồm 2 chữ số sau một đơn vị.

Giải:

Đặt ta có và

=>

=> hoặc

Mà

Vì nên

=>

=>

Ví dụ 2: Tập hợp các chữ số tận cùng có thể có của một số chính phương là {}
(Nhập các phần tử theo thứ tự tăng dần,cách nhau bởi dấu “;”)

Giải:

Ta có: 1 số chính phương = a².

Trong đó chữ số tận cùng của số chính phương đó = chữ số tận cùng của a nhân với chính nó.

Mà a có thể có tận cùng ={0;1;2;3;4;5;6;7;8;9} => a² có thể có tận cùng bằng: 1;0;4;9;5;6.

Vậy tập hợp các chữ số tận cùng của 1 số chính phương có thể là: {0;1;4;9;5;6}.
Sotayhoctap chúc các bạn học tốt!