Công thức cấp số nhân: công thức tính cấp số nhân, công thức tính tổng cấp số nhân, tổng của cấp số nhân, tổng cấp số nhân lùi vô hạn…

Định nghĩa cấp số nhân

Dãy số (un) được xác định bởi $\left\{ {\begin{array}{*{20}{c}}{{u_1} = a}\\{{u_{n + 1}} = {u_n}.q}\end{array}} \right.,{\rm{ }}n \in {N^*}$ gọi là cấp số cộng; $q$ gọi là công bội.

Các tính chất cấp số nhân

$\bullet$ Số hạng thứ n được cho bởi công thức: ${u_n} = {u_1}{q^{n - 1}}$ .

$\bullet$ Ba số hạng ${u_k},{u_{k + 1}},{u_{k + 2}}$ là ba số hạng liên tiếp của cấp số cộng khi và chỉ khi $u_{k + 1}^2 = {u_k}.{u_{k + 2}}$ .

$\bullet$ Tổng $n$ số hạng đầu tiên ${S_n}$ được xác định bởi công thức :

${S_n} = {u_1} + {u_2} + ... + {u_n} = {u_1}\frac{{{q^n} - 1}}{{q - 1}}$ .

Công bội q của cấp số nhân

Công bội q của cấp số nhân $(u_{1})$ được tính bằng công thức:

$q=\frac{u_{n+1}}{u_{n}}$

Ví dụ: Cho cấp số nhân $(u_{n})$ có $(u_{1})$ =2 , $(u_{2})$ = 4. Tính công bội q.

Lời giải: Áp dụng công thức tính công bội q ta có:

$q=\frac{u_{2}}{u_{1}}=\frac{4}{2}=2$

Số hạng tổng quát của cấp số nhân

Nếu cấp số nhân có số hạng đầu $(u_{1})$ và công bội q thì số hạng tổng quát $(u_{n})$ được tính bởi công thức:

$u_{n}=u_{1}.q^{n-1}$ ới $n\geq 2$

Ví dụ: Cho cấp số nhân $(u_{n})$ với $(u_{1})$ = 3, $q=\frac{-1}{2}$ . Tính $(u_{7})$

Lời giải: $u_{7}=u_{1}.q^{7-1}$ =3. $(\frac{-1}{2})^{6}$ = $\frac{3}{64}$

Tổng n số hạng đầu tiên

$S_{n} = u_{1} + u_{2} + … + u_{n} = u_{1}\frac{1 - q^{n}}{1 - q} (q\neq 1)$

Nếu q = 1 thì cấp số nhân là $S_{n} = n.u_{1}$

Ví dụ: Cho cấp số nhân $(u_{n})$ biết $(u_{1})$ = 2, $(u_{3})$ = 18. Tính tổng của 10 số hạng đầu tiên.

Lời giải: Ta có $u_{3}=q^{2}.u_{1}=2.q^{2}=18$

Suy ra q = 3 hoặc q= -3

Với q =3 ta có $S_{10}=\frac{10_{1}(1-3^10)}{1-3}$ = 59048

Với q=-3 ta có $S_{10}=\frac{10_{1}(1-3^10)}{1+3}$ = -29524

Cấp số nhân lùi vô hạn

$(u_{n})$ có công bội q, |q|<1 được gọi là cấp số nhân lùi vô hạn.

Ví dụ: $\frac{1}{2}, \frac{1}{4}, \frac{1}{8}, \frac{1}{16}$ ,… là một cấp số nhân lùi vô hạn với công bội $q=\frac{1}{2}$

Tổng của cấp số nhân lùi vô hạn

Cho cấp số nhân lùi vô hạn $(u_{n})$ có công bội q. Khi đó ta có tổng của cấp số nhân lùi vô hạn S bằng:

$S=\frac{u_{1}}{1-q}$ với |q| < 1

Ví dụ: Tính tổng của cấp số nhân lùi vô hạn $(u_{n})$ với $u_{n}=\frac{1}{3^{n}}$

Lời giải: Ta có $u_{1}=\frac{1}{3}$ , $u_{2}=\frac{1}{9}$ .

Suy ra $q=\frac{1}{3}$ .

Áp dụng công thức tính tổng cấp số nhân lùi vô hạn ta có:

$S=\frac{u_{1}}{1-q}$

$S=\frac{\frac{1}{3}}{1-\frac{1}{3}}=\frac{1}{2}$

Bài tập minh họa cấp số nhân

Vấn đề 1: Xác định cấp số và xác yếu tố của cấp số nhân

Phương pháp:

$\bullet$ Dãy số $({u_n})$ là một cấp số nhân $\Leftrightarrow \frac{{{u_{n + 1}}}}{{{u_n}}} = q$ không phụ thuộc vào n và $q$ là công bội.

$\bullet$ Ba số $a,b,c$ theo thứ tự đó lập thành cấp số nhân $\Leftrightarrow ac = {b^2}$ .

$\bullet$ Để xác định một cấp số nhân, ta cần xác định số hạng đầu và công bội. Do đó, ta thường biểu diễn giả thiết của bài toán qua ${u_1}$ và $q$ .

Ví dụ 1:

Cho cấp số nhân (un) có các số hạng khác không, tìm ${u_1}$ biết:

a) $\left\{ {\begin{array}{*{20}{c}}{{u_1} + {u_2} + {u_3} + {u_4} = 15}\\{u_1^2 + u_2^2 + u_3^2 + u_4^2 = 85}\end{array}} \right.$

b) $\left\{ {\begin{array}{*{20}{c}}{{u_1} + {u_2} + {u_3} + {u_4} + {u_5} = 11}\\{{u_1} + {u_5} = \frac{{82}}{{11}}}\end{array}} \right.$

Hướng dẫn:

a) Ta có: 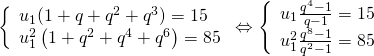$\left\{ \begin{array}{l}{u_1}(1 + q + {q^2} + {q^3}) = 15\\u_1^2\left( {1 + {q^2} + {q^4} + {q^6}} \right) = 85\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{u_1}\frac{{{q^4} - 1}}{{q - 1}} = 15\\u_1^2\frac{{{q^8} - 1}}{{{q^2} - 1}} = 85\end{array} \right.$

$\Rightarrow {\left( {\frac{{{q^4} - 1}}{{q - 1}}} \right)^2}\left( {\frac{{{q^2} - 1}}{{{q^8} - 1}}} \right) = \frac{{45}}{{17}} \Leftrightarrow \frac{{({q^4} - 1)(q + 1)}}{{(q - 1)({q^4} + 1)}} = \frac{{45}}{{17}} \Leftrightarrow \left[ \begin{array}{l}q = 2\\q = \frac{1}{2}\end{array} \right.$

Từ đó ta tìm được ${u_1} = 1,{u_1} = 8$ .

b) Ta có: $\left\{ \begin{array}{l}{u_1}\left( {1 + q + {q^2} + {q^3} + {q^4}} \right) = 11\\{u_1}(1 + {q^4}) = \frac{{82}}{{11}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{u_1}q(1 + q + {q^2}) = \frac{{39}}{{11}}\\{u_1}(1 + {q^4}) = \frac{{82}}{{11}}\end{array} \right.$

$\Rightarrow \frac{{{q^4} + 1}}{{{q^3} + {q^2} + q}} = \frac{{82}}{{39}} \Leftrightarrow q = 3,q = \frac{1}{3}$ .

Ví dụ 2:

Cho cấp số nhân $({u_n})$ thỏa: $\left\{ \begin{array}{l}{u_4} = \frac{2}{{27}}\\{u_3} = 243{u_8}\end{array} \right.$ .

a) Viết năm số hạng đầu của cấp số.

b) Tính tổng 10 số hạng đầu của cấp số.

c) Số $\frac{2}{{6561}}$ là số hạng thứ bao nhiêu của cấp số?

Hướng dẫn:

Gọi $q$ là công bội của cấp số. Theo giả thiết ta có:

$\left\{ \begin{array}{l}{u_1}{q^3} = \frac{2}{{27}}\\{u_1}{q^2} = 243.{u_1}{q^7}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{u_1}{q^3} = \frac{2}{{27}}\\{q^5} = \frac{1}{{243}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}q = \frac{1}{3}\\{u_1} = 2\end{array} \right.$

a) Năm số hạng đầu của cấp số là: ${u_1} = 2,{u_2} = \frac{2}{3},{u_3} = \frac{2}{9};{u_4} = \frac{2}{{27}},{u_5} = \frac{2}{{81}}$ .

b) Tổng 10 số hạng đầu của cấp số

${S_{10}} = {u_1}\frac{{{q^{10}} - 1}}{{q - 1}} = 2.\frac{{{{\left( {\frac{1}{3}} \right)}^{10}} - 1}}{{\frac{1}{3} - 1}} = 3\left[ {1 - {{\left( {\frac{1}{3}} \right)}^{10}}} \right] = \frac{{59048}}{{19683}}$ .

c) Ta có: ${u_n} = \frac{2}{{{3^{n - 1}}}} \Rightarrow {u_n} = \frac{2}{{6561}} \Leftrightarrow {3^{n - 1}} = 6561 = {3^8} \Rightarrow n = 9$

Vậy $\frac{2}{{6561}}$ là số hạng thứ 9 của cấp số.

Vấn đề 3: Tìm điều kiện để dãy số lập thành cấp số nhân

Phương pháp: $a,b,c$ theo thứ tự đó lập thành CSN $\Leftrightarrow ac = {b^2}$ .

Ví dụ 1: Tìm $x$ biết $1,{x^2},6 - {x^2}$ lập thành cấp số nhân.

Hướng dẫn:

Ta có: $1,{x^2},6 - {x^2}$ lập thành cấp số nhân $\Leftrightarrow {x^4} = 6 - {x^2} \Leftrightarrow x = \pm \sqrt 2 .$

Ví dụ 2: Tìm $x,y$ biết:

a) Các số $x + 5y,5x + 2y,8x + y$ lập thành cấp số cộng và các số

${\left( {y - 1} \right)^2},xy - 1,{\left( {x + 1} \right)^2}$ lập thành cấp số nhân.

b) Các số $x + 6y,5x + 2y,8x + y$ lập thành cấp số cộng và các số $x + \frac{5}{3}y,y - 1,2x - 3y$ lập thành cấp số nhân.

Hướng dẫn:

a) Ta có hệ: $\left\{ \begin{array}{l}x + 5y + 8x + y = 2(5x + 2y)\\{(x + 1)^2}{(y - 1)^2} = {(xy - 1)^2}\end{array} \right.$ giải hệ này ta tìm được

$(x;y) = \left( { - \sqrt 3 ; - \frac{{\sqrt 3 }}{2}} \right);\left( {\sqrt 3 ;\frac{{\sqrt 3 }}{2}} \right)$ .

b) Ta có hệ: $\left\{ \begin{array}{l}x + 6y + 8x + y = 2(5x + 2y)\\(x + \frac{5}{3}y)(2x - 3y) = {(y - 1)^2}\end{array} \right.$ giải hệ này ta tìm được

$(x;y) = \left( { - 3; - 1} \right);\left( {\frac{3}{8};\frac{1}{8}} \right)$ .

Mời các bạn xem thêm video bài giảng về “Cấp số nhân”:

Trên đây là bài viết công thức cấp số nhân, chúc các bạn làm bài tốt!

2.3/5 - (25 bình chọn)

SỔ TAY HỌC TẬP | SOTAYHOCTAP.COM

Công thức cấp số nhân nâng cao | Lý thuyết + bài tập ví dụ

Định nghĩa cấp số nhân

Các tính chất cấp số nhân

Công bội q của cấp số nhân

Số hạng tổng quát của cấp số nhân

Tổng n số hạng đầu tiên

Cấp số nhân lùi vô hạn

Tổng của cấp số nhân lùi vô hạn

Bài tập minh họa cấp số nhân

Định nghĩa cấp số nhân

Các tính chất cấp số nhân

Công bội q của cấp số nhân

Số hạng tổng quát của cấp số nhân

Tổng n số hạng đầu tiên

Cấp số nhân lùi vô hạn

Tổng của cấp số nhân lùi vô hạn

Bài tập minh họa cấp số nhân

Related Posts

Chuyên đề số chính phương

Lược đồ Hoocne (Sơ đồ Hoocne) trong cách chia đa thức

Nhị thức Newton, cách khai triển và một số dạng bài tập áp dụng

Những hằng đẳng thức đáng nhớ, hằng đẳng thức mở rộng và dạng toán áp dụng

Hàm số liên tục và bài toán xét tính liên tục của hàm số

Cách tìm tập xác định của hàm số mũ và hàm số logarit