Công thức định lý pitago – Định lý pitago đảo

Bài viết định lý pitago bao gồm: công thức định lý pitago, ví dụ bài tập định lý pitago…

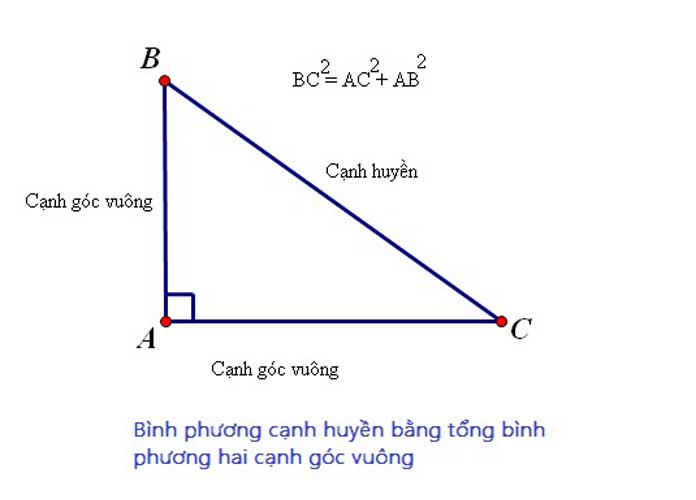
Định lý pitago

Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng bình phương hai cạnh góc vuông.

∆ABC vuông tại A.

=> BC²=AB²+AC²

Định lý pitago đảo

Nếu một tam giác có bình phương của một cạnh bẳng tổng bình phương các cạnh còn lại thì tam giác đó là tam giác vuông.
∆ABC :BC²=AB²+AC²

=> = 90²

Ví dụ bài tập định lý pitago

Ví dụ 1: Cho tam giác nhọn ABC. Kẻ AH vuông góc với BC(H thuộc BC), cho biết AB=13,AH=12,hc=16 cm. Tính độ dài các cạnh của tam giác ABC.
Lời giải:
Ta có:
AC²= AH²+HC²=12²+16²=144+156=400.
=> AC=20(cm )

BH²=AB²-AH²=13²-12²
=169 – 144 = 25 => BH=5(cm)
Do đó BC=BH+HC=5+16=21(cm)

Ví dụ 2: Bạn Tâm muốn đóng cho một nẹp chéo AC để khung hình chữ nhật ABCD được vững hơn(h.134). Tính độ dài AC, Biết rằng AD=48 cm, CD=36 cm.

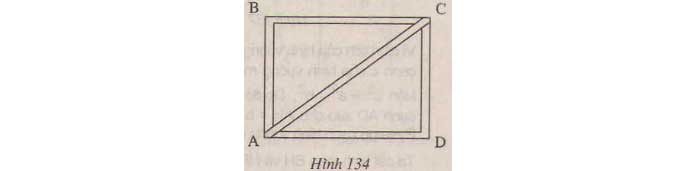
Lời giải:

Theo định lí Pytago, ta có:
AC²= AD² +CD²
= 48² + 36²
= 2304 + 1296= 3600
AC= 60 (cm)
Sotayhoctap chúc các bạn học tốt!