Công thức tích phân từng phần: Công thức, ví dụ và cách tính tích phân từng phần…
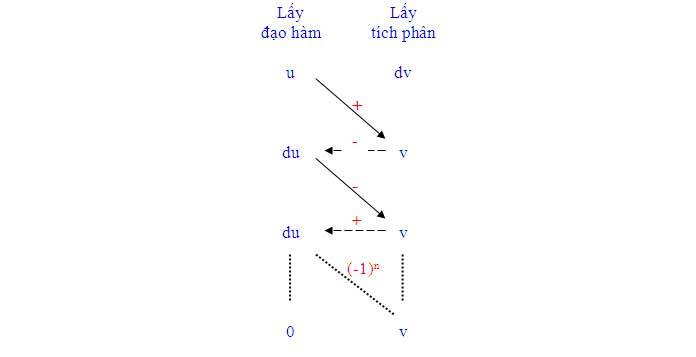
Công thức tích phân từng phần
Cho hai hàm số u và v có đạo hàm liên tục trên đoạn [a, b], thì ta có :
![]()
Trong lúc tính tính tích phân từng phần ta có những ưu tiên sau :
Ưu tiên 1: Nếu có hàm ln hay logarit thì phải đặt u = ln(x) hay u = log![]() x.
x.
Ưu tiên 2 : Đặt u = ? mà có thể hạ bậc.
Ví dụ áp dụng công thức tích phân từng phần
Ví dụ 1: Tính các tích phân sau :
a) ![]()
b) ![]()
c) ![]()
Lời giải:
a) Đặt: ![]()
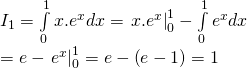
b) Đặt: ![]()
Vậy: 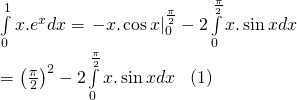
Ta đi tính tích phân ![]()
Đặt: ![]()
Vậy: 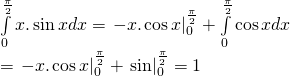
Thế vào (1) ta được: ![]()
c) Đặt:
![]()
Vậy: ![]()
Ví dụ 2: Tính các tích phân sau
a) ![]()
b) ![]()
c) ![]()
Lời giải:
a) Đặt: ![]()
Vậy: 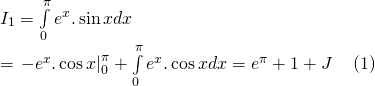
Đặt: ![]()
Vậy: ![]()
Thế vào (1) ta được: ![]()
b) Đặt: ![]()
Vậy: ![]()
c) Đặt: ![]()
Vậy: 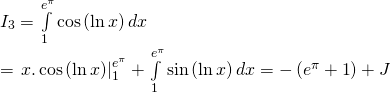
Đặt:
![]()
Vậy: 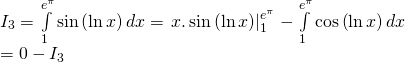
Thế vào (1) ta được: ![]()
Sotayhoctap chúc các bạn học tốt!




