Diện tích tam giác là gì? Công thức tính diện tích tam giác, cách tính diện tích tam giác.

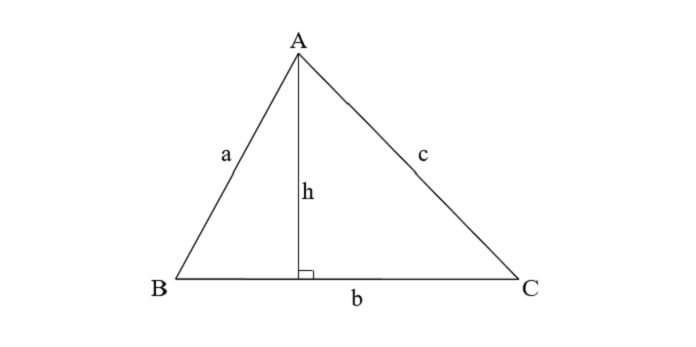
Định nghĩa diện tích tam giác

Diện tích tam giác bằng 1 phần 2 tích của chiều cao hạ từ đỉnh với độ dài cạnh đối diện của đỉnh đó.

Công thức tính diện tích tam giác

1. Công thức tính diện tích tam giác thường

a) ${S_{ABC}} = \frac{1}{2}a.{h_a} = \frac{1}{2}b.{h_b} = \frac{1}{2}c.{h_c}$

(hay nói cách khác Diện tích tam giác bằng 1 phần 2 tích của chiều cao hạ từ đỉnh với độ dài cạnh đối diện của đỉnh đó)

b) ${S_{ABC}} = \frac{1}{2}a.b.\sin C = \frac{1}{2}a.c.\sin B = \frac{1}{2}b.c.\sin A$

(Diện tích tam giác bằng 1 phần 2 tích 2 cạnh và sin của góc hợp bởi 2 cạnh đó trong tam giác)

c) ${S_{ABC}} = \sqrt {p(p - a)(p - b)(p - c)}$

(công thức Hê rông – p là nửa chu vi của tam giác, a, b, c là độ dài của 3 cạnh trong tam giác)

d) ${S_{ABC}} = p.r$

(p là nửa chu vi của tam giác, r là bán kính đường tròn nội tiếp tam giác)

e) ${S_{ABC}} = \frac{{abc}}{{4R}}$

(R là bán kính đường tròn ngoại tiếp tam giác, a, b, c là độ dài 3 cạnh của tam giác)

f) ${S_{ABC}} = 2.{R^2}.\sin A.\sin B.\sin C$

(sử dụng công thức cần phải chứng minh, R là bán kính đường tròn ngoại tiếp tam giác, A, B, C là 3 góc của tam giác).

* Một số chú ý khi tính diện tích tam giác.

– Với tam giác có chứa góc bẹt chiều cao nằm bên ngoài tam giác.

– Khi tính diện tích tam giác chiều cao nào ứng với đáy đó.

– Nếu hai tam giác có chung chiều cao hoặc chiều cao bằng nhau -> diện tích hai tam giác tỉ lệ với 2 cạnh đáy và ngược lại nếu hai tam giác có chung đáy (hoặc hai đáy bằng nhau) -> diện tích tam giác tỉ lệ với 2 đường cao tương ứng.

2. Công thức tính diện tích tam giác vuông

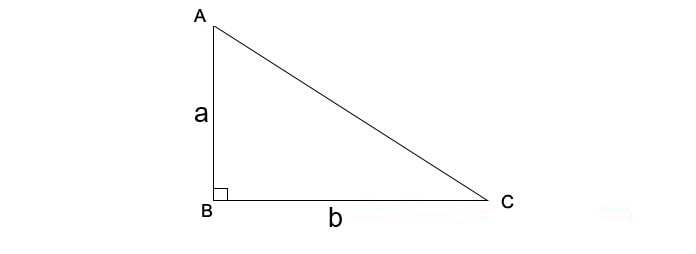
Có thể áp dụng các công thức tính diện tích tam giác thường cho tam giác vuông tương ứng. Ngoài ra để rút gọn bạn có thể sử dụng các công thức tính diện tích riêng biệt cho tam giác vuông như sau:

${S_{ABC}} = \frac{1}{2}a.b$ (với a, b là độ dài hai cạnh góc vuông)

3. Công thức tính diện tích tam giác cân

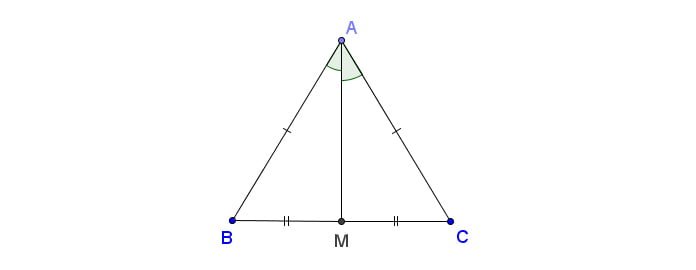
${S_{ABC}} = \frac{1}{2}a.{h_a}$ (Với a là độ dài cạnh đáy tương ứng với đường cao kẻ từ cạnh đối diện, ha là độ dài đường cao tương ứng)

4. Công thức tính diện tích tam giác đều

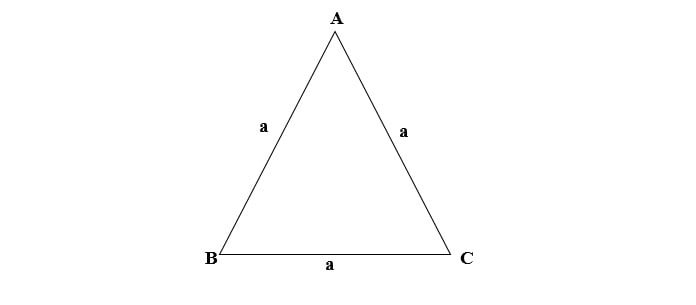
${S_{ABC}} = {a^2}.\frac{{\sqrt 3 }}{4}$ (Với a là độ dài cạnh của tam giác)

5. Diện tích tam giác vuông cân

Do tam giác vuông cân có cạnh đáy bằng chiều cao nên diện tích tam giác được tính bằng một nửa bình phương cạnh đáy hoặc 1 nửa bình phương chiều cao.

$S=\frac{1}{2}a^{2}$

Với a là độ dài cạnh đáy

Ví dụ cách tính diện tích tam giác

Ví dụ 1:

Cho tam giác ABC (như hình vẽ) có độ dài đáy BC = 16, diện tích tam giác là 200 cm2. Vẽ chiều cao AH và tính AH.

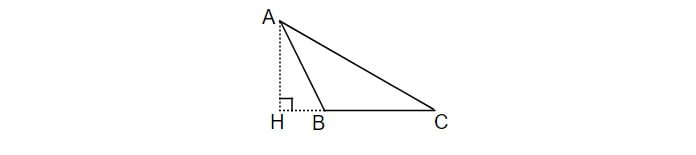
Lời giải:

+) Đáy là BC thì chiều cao là đoạn thẳng xuất phát từ A và vuông góc với BC.

+) Áp dụng công thức tính chiều cao h = S x 2 : a.

Độ dài chiều cao AH là: 200 x 2 : 16 = 25 (cm)

Đáp số: 25 cm

Nhận xét :

– Không phải lúc nào chiều cao cũng nằm trong tam giác.
– Khi tính diện tích tam giác, cần lưu ý: Chiều cao nào thì phải ứng với đáy đó.(Trong ví dụ 1, đáy là BC thì chiều cao là AH).

Ví dụ 2:

Cho tam giác ABC có diện tích là 45 cm2. D là trung điểm của cạnh AB. Trên cạnh AC lấy điểm E sao cho AE gấp đôi EC. Tính diện tích tam giác AED.

Lời giải:

Nối B với E. Vẽ EH vuông góc với AB.

Ta có

S_ABE = $\frac{1}{2}$ x EH x AB

S_ADE = $\frac{1}{2}$ x EH x AD

= $\frac{1}{2}$ x EH x $\frac{1}{2}$ x AB (vì AD = $\frac{1}{2}$ x AB)

= $\frac{1}{2}$ x SABE (1)

Tương tự, ta có: ABE và ABC là hai tam giác có chung chiều cao hạ từ đỉnh B mà đáy AE = $\frac{2}{3}$ x AC

Suy ra: SABE = $\frac{2}{3}$ x SABC (2) .

Từ (1) và (2) ta có S_ADE = $\frac{1}{2}$ x $\frac{2}{3}$ x SABC = $\frac{1}{3}$ x 45 = 15 (cm2)

Đáp số : 15 cm2

Nhận xét:

– Ta có thể tính diện tích tam giác bằng cách tìm mối quan hệ giữa các tam giác.

+ Nếu hai tam giác có chung chiều cao (hoặc chiều cao bằng nhau) thì diện tích của chúng tỉ lệ với hai cạnh đáy .

+ Nếu hai tam giác có chung đáy (hoặc đáy bằng nhau) thì diện tích của chúng tỉ lệ với hai đường cao tương ứng.

– Lưu ý: Ưu tiên nối thêm hình và chọn đáy là những cạnh có chia tỉ lệ. (Ở ví dụ 2, ta cũng có thể nối D với C).
Sotayhoctap chúc các bạn học tốt!

5/5 - (2 bình chọn)

SỔ TAY HỌC TẬP | SOTAYHOCTAP.COM

Công thức tính diện tích tam giác đầy đủ | Lý thuyết + bài tập ví dụ

Định nghĩa diện tích tam giác

Công thức tính diện tích tam giác

1. Công thức tính diện tích tam giác thường