Bài viết hàm số liên tục bao gồm: định lý và định nghĩa về hàm số liên tục, xét tính liên tục của hàm số, bài tập hàm số liên tục có lời giải, hàm số liên tục trên khoảng, hàm số liên tục tại 1 điểm…
Lý thuyết hàm số liên tục
Hàm số liên tục là gì?
Định nghĩa 1: Cho hàm số ![]() xác định trên khoảng
xác định trên khoảng ![]() . Hàm số
. Hàm số ![]() được gọi là liên tục tại
được gọi là liên tục tại ![]() nếu
nếu ![]() .
.
Hàm số ![]() không liên tục tại
không liên tục tại ![]() được gọi là gián đoạn tại điểm đó.
được gọi là gián đoạn tại điểm đó.
Chú ý: Khi xét tính liên tục của hàm số tại một điểm, đặc biệt chú ý đến điều kiện hàm số xác định trên một khoảng (dù nhỏ) chứa điểm đó.
Định nghĩa 2: Hàm số ![]() được gọi là liên tục trên một khoảng nếu nó liên tục tại mọi điểm của khoảng đó.
được gọi là liên tục trên một khoảng nếu nó liên tục tại mọi điểm của khoảng đó.
Hàm số ![]() được gọi là liên tục trên một đoạn
được gọi là liên tục trên một đoạn ![]() nếu nó liên tục trên khoảng
nếu nó liên tục trên khoảng ![]() và
và ![]() .
.
Chú ý: Đồ thị của hàm số liên tục trên một khoảng là một đường liền trên khoảng đó.
Các định lý về hàm số liên tục
Định lý 1: Tổng, hiệu, tích, thương của hai hàm số liên tục tại một điểm là những hàm số liên tục tại điểm đó (trong trường hợp thương, giá trị của mẫu tại điểm đó phải khác ![]() ).
).
Định lý 2:
a) Hàm đa thức liên tục trên ![]() .
.
b) Hàm phân thức hữu tỉ, hàm lượng giác liên tục trên từng khoảng của tập xác định.
c) Các hàm số sơ cấp liên tục trên từng khoảng xác định của chúng.
Định lý 3: Nếu hàm số ![]() lên tục trên đoạn
lên tục trên đoạn ![]() và
và ![]() thì tồn tại ít nhất một điểm
thì tồn tại ít nhất một điểm ![]() sao cho
sao cho ![]() .
.
Chú ý: Nếu ![]() liên tục trên đoạn
liên tục trên đoạn ![]() và
và ![]() thì phương trình
thì phương trình ![]() có ít nhất một nghiệm nằm trong khoảng
có ít nhất một nghiệm nằm trong khoảng ![]() .
.
Hàm số liên tục tại một điểm
![]() liên tục tại
liên tục tại ![]()
– Để xét tính liên tục của hàm số ![]() tại điểm
tại điểm ![]() ta thực hiện các bước:
ta thực hiện các bước:
Bước 1: Tính ![]() .
.
Bước 2: Tính ![]() (trong nhiều trường hợp ta cần tính
(trong nhiều trường hợp ta cần tính ![]() ,
, ![]() )
)
Bước 3: So sánh ![]() với
với ![]() và rút ra kết luận.
và rút ra kết luận.
Bước 4: Kết luận.
Hàm số liên tục trên một khoảng
![]() liên tục tại mọi điểm thuộc khoảng đó.
liên tục tại mọi điểm thuộc khoảng đó.
Hàm số liên tục trên một đoạn ![Rendered by QuickLaTeX.com [a; b]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIzMSIgaGVpZ2h0PSIxOCIgdmlld0JveD0iMCAwIDMxIDE4Ij48cmVjdCB3aWR0aD0iMTAwJSIgaGVpZ2h0PSIxMDAlIiBmaWxsPSIjY2ZkNGRiIi8+PC9zdmc+)
![]() liên tục trên
liên tục trên ![]() và
và ![]() .
.
Hàm số đa thức liên tục trên  .
.
Hàm số phân thức, các hàm số lượng giác liên tục trên từng khoảng xác định của chúng.
Giả sử  liên tục tại điểm
liên tục tại điểm  .
.
Khi đó:
– Các hàm số ![]() liên tục tại
liên tục tại ![]() .
.
– Hàm số ![]() liên tục tại
liên tục tại ![]() nếu
nếu ![]() .
.
Nếu  liên tục trên
liên tục trên ![Rendered by QuickLaTeX.com [a; b]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIzMSIgaGVpZ2h0PSIxOCIgdmlld0JveD0iMCAwIDMxIDE4Ij48cmVjdCB3aWR0aD0iMTAwJSIgaGVpZ2h0PSIxMDAlIiBmaWxsPSIjY2ZkNGRiIi8+PC9zdmc+) và
và  thì tồn tại ít nhất một số
thì tồn tại ít nhất một số  .
.
Nói cách khác: Nếu ![]() liên tục trên
liên tục trên ![]() và
và ![]() thì phương trình
thì phương trình ![]() có ít nhất một nghiệm
có ít nhất một nghiệm ![]() .
.
Mở rộng: Nếu ![]() liên tục trên [a; b]. Đặt
liên tục trên [a; b]. Đặt ![]() ,
, ![]() . Khi đó với mọi
. Khi đó với mọi ![]() luôn tồn tại ít nhất một số
luôn tồn tại ít nhất một số ![]() :
: ![]() .
.
Một số dạng toán về hàm số liên tục
Xét tính liên tục của hàm số.
– Bước 1: Tính ![]() và
và ![]()
– Bước 2: So sánh và kết luận.
+) Nếu ![]() thì hàm số liên tục tại
thì hàm số liên tục tại ![]() .
.
+) Nếu ![]() không tồn tại hoặc
không tồn tại hoặc ![]() thì kết luận hàm số không liên tục tại
thì kết luận hàm số không liên tục tại ![]() .
.
Vấn đề 1: Hàm số liên tục tại một điểm
Dạng 1: 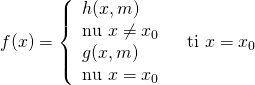
Phương pháp:
Bước 1: Tính ![]() .
.
Bước 2: Tính ![]() .
.
Bước 3: So sánh ![]() với
với ![]() và rút ra kết luận.
và rút ra kết luận.
Bước 4: Kết luận.
Ví dụ: Xét tính liên tục của hàm số tại điểm được chỉ ra: 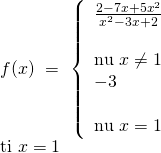
Hướng dẫn giải:
![]()
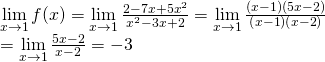
Do: ![]() nên hàm số
nên hàm số ![]() liên tục tại
liên tục tại ![]()
Vậy: Hàm số ![]() liên tục tại
liên tục tại ![]()
Dạng 2: 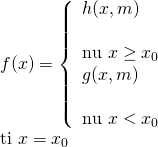 hoặc
hoặc 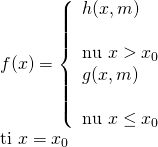
Phương pháp:
Bước 1: Tính ![]() .
.
Bước 2: Tính ![]() ,
, ![]() .
.
Bước 3: So sánh ![]() ,
, ![]() với
với ![]() và rút ra kết luận.
và rút ra kết luận.
Bước 4: Kết luận.
Ví dụ: Xét tính liên tục của hàm số tại điểm được chỉ ra: 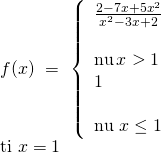
Hướng dẫn giải:
![]()
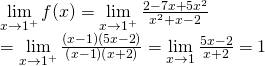
![]()
Do: ![]() nên hàm số
nên hàm số ![]() liên tục tại
liên tục tại ![]()
Vậy: Hàm số ![]() liên tục tại
liên tục tại ![]()
Dạng 3: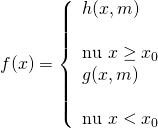 hoặc
hoặc 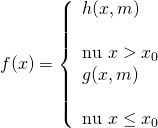
Phương pháp:
Bước 1: Tìm tập xác định của hàm số.
Bước 2: Khi ![]() . Kiểm tra tính liên tục của hàm số
. Kiểm tra tính liên tục của hàm số ![]() trên các khoàng.
trên các khoàng.
Bước 3: Khi ![]() .
.
– Tính ![]() .
.
– Tính ![]() ,
, ![]() .
.
– So sánh ![]() ,
, ![]() với
với ![]() và rút ra kết luận tại điểm
và rút ra kết luận tại điểm ![]() .
.
Bước 4: Kết luận tính liên tục trên tập xác định của chúng.
Ví dụ: Xét tính liên tục của hàm số trên tập xác định của chúng: 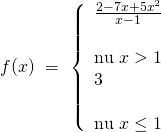
Hướng dẫn giải:
– Tập xác định: ![]() .
.
– Nếu ![]() , thì hàm số
, thì hàm số ![]() .
.
Đây là hàm phân thức hữu tỉ có tập xác định là ![]() .
.
Vậy nó liên tục trên mỗi khoảng ![]() .
.
– Nếu ![]() , thì hàm số
, thì hàm số ![]() .
.
Đây là hàm đa thức có tập xác định là ![]() .
.
Vậy nó liên tục trên mỗi khoảng ![]() .
.
– Nếu ![]()
![]()
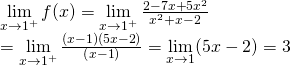
![]()
Do: ![]() nên hàm số f(x) liên tục tại
nên hàm số f(x) liên tục tại ![]()
Vậy: Hàm số ![]() liên tục tại
liên tục tại ![]()
– Vậy: Hàm số ![]() liên tục trên
liên tục trên ![]() .
.
Vấn đề 2: Hàm số liên tục trên tập xác định của nó
Dạng 1: 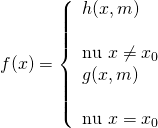
Phương pháp:
Bước 1: Tìm tập xác định của hàm số.
Bước 2: Khi ![]() . Kiểm tra tính liên tục của hàm số
. Kiểm tra tính liên tục của hàm số ![]() tại
tại ![]() .
.
Bước 3: Khi ![]() .
.
– Tính ![]() .
.
– Tính ![]() .
.
– So sánh ![]() với
với ![]() và rút ra kết luận tại điểm
và rút ra kết luận tại điểm ![]() .
.
Bước 4: Kết luận tính liên tục trên tập xác định của chúng.
Ví dụ: Xét tính liên tục của hàm số trên tập xác định của chúng: 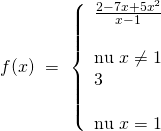
Hướng dẫn giải:
– Tập xác định: ![]()
– Nếu ![]() , thì hàm số
, thì hàm số ![]() .
.
Đây là hàm phân thức hữu tỉ có tập xác định là ![]() .
.
Vậy nó liên tục trên mỗi khoảng ![]() và
và ![]()
– Nếu ![]()
![]()
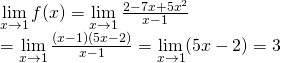
Do: ![]() nên hàm số
nên hàm số ![]() liên tục tại
liên tục tại ![]()
Suy ra hàm số f(x) liên tục tại ![]()
– Vậy: Hàm số ![]() liên tục trên
liên tục trên ![]() .
.
Dạng 2: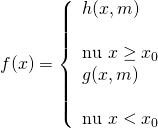 hoặc
hoặc 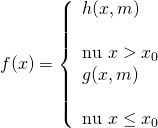
Phương pháp:
Bước 1: Tìm tập xác định của hàm số.
Bước 2: Khi ![]() . Kiểm tra tính liên tục của hàm số
. Kiểm tra tính liên tục của hàm số ![]() trên các khoàng.
trên các khoàng.
Bước 3: Khi ![]() .
.
– Tính ![]() .
.
– Tính ![]() ,
, ![]() .
.
– So sánh ![]() ,
, ![]() với
với ![]() và rút ra kết luận tại điểm
và rút ra kết luận tại điểm ![]() .
.
Bước 4: Kết luận tính liên tục trên tập xác định của chúng.
Ví dụ: Xét tính liên tục của hàm số trên tập xác định của chúng: 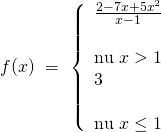
Hướng dẫn giải:
– Tập xác định: ![]() .
.
– Nếu ![]() , thì hàm số
, thì hàm số ![]() .
.
Đây là hàm phân thức hữu tỉ có tập xác định là ![]() .
.
Vậy nó liên tục trên mỗi khoảng ![]() .
.
– Nếu ![]() , thì hàm số
, thì hàm số ![]() .
.
Đây là hàm đa thức có tập xác định là ![]() .
.
Vậy nó liên tục trên mỗi khoảng ![]() .
.
– Nếu ![]()
![]()
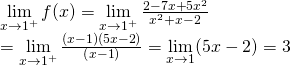
![]()
Do: ![]() nên hàm số f(x) liên tục tại
nên hàm số f(x) liên tục tại ![]()
Vậy: Hàm số ![]() liên tục tại
liên tục tại ![]()
– Vậy: Hàm số ![]() liên tục trên
liên tục trên ![]() .
.
Chứng minh phương trình có nghiệm
Phương pháp:
– Bước 1: Chứng minh hàm số ![]() liên tục trên đoạn
liên tục trên đoạn ![]() .
.
– Bước 2: Chứng minh ![]() .
.
– Bước 3: Kết luận phương trình ![]() có ít nhất một nghiệm trên đoạn
có ít nhất một nghiệm trên đoạn ![]() .
.
Chú ý: Đối với bài toán chứng minh phương trình ![]() có nghiệm mà không cho khoảng nào thì ta cần tìm hai số
có nghiệm mà không cho khoảng nào thì ta cần tìm hai số ![]() sao cho
sao cho ![]() .
.
Ví dụ: Chứng minh phương trình ![]() có nghiệm trong khoảng
có nghiệm trong khoảng ![]()
Hướng dẫn giải:
– Xét hàm số ![]() là hàm đa thức, liên tục trên R tức liên tục trên khoảng
là hàm đa thức, liên tục trên R tức liên tục trên khoảng ![]() .
.
– Ta có: ![]() .
.
– Do đó: ![]() , tức phương trình có nghiệm
, tức phương trình có nghiệm ![]() .
.
Ví dụ bài tập hàm số liên tục có lời giải
Bài tập 1: Xét tính liên tục của hàm số tại điểm được chỉ ra: 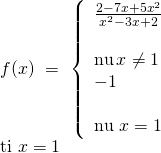
Hướng dẫn giải:
![]()
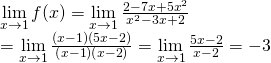
Do: ![]() nên hàm số
nên hàm số ![]() gián đoạn tại
gián đoạn tại ![]()
Vậy: Hàm số ![]() gián đoạn tại
gián đoạn tại ![]()
Bài tập 2: Tìm m để hàm số liên tục tại điểm được chỉ ra: 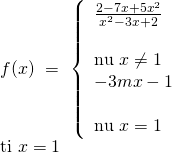
Hướng dẫn giải:
![]()
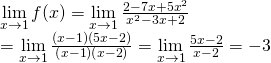
Để hàm số ![]() liên tục tại
liên tục tại 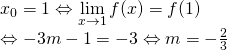
Vậy: Giá trị ![]() cần tìm là
cần tìm là ![]()
Bài tập 3: Xét tính liên tục của hàm số tại điểm được chỉ ra: 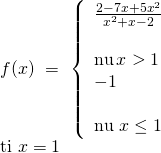
Hướng dẫn giải:
![]()
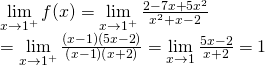
![]()
Do: ![]() nên hàm số f(x) gián đoạn tại
nên hàm số f(x) gián đoạn tại ![]()
Vậy: Hàm số ![]() gián đoạn tại
gián đoạn tại ![]()
Bài tập 4: Tìm m để hàm số liên tục tại điểm được chỉ ra: 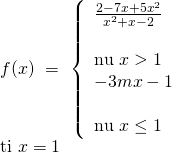
Hướng dẫn giải:
![]()
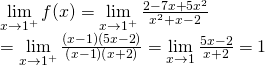
![]()
Do hàm số ![]() liên tục tại
liên tục tại 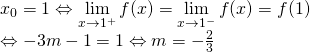
Vậy: Giá trị ![]() cần tìm là:
cần tìm là: ![]()
Bài tập 5: Xét tính liên tục của hàm số trên tập xác định của chúng: 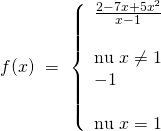
Hướng dẫn giải:
– Tập xác định: ![]()
– Nếu ![]() , thì hàm số
, thì hàm số ![]() .
.
Đây là hàm phân thức hữu tỉ có tập xác định là ![]() .
.
Vậy nó liên tục trên mỗi khoảng ![]() và
và ![]()
– Nếu ![]()
![]()
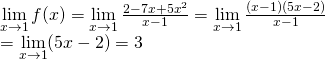
Do: ![]() nên hàm số
nên hàm số ![]() không liên tục tại
không liên tục tại ![]()
Suy ra hàm số ![]() không liên tục tại
không liên tục tại ![]()
– Vậy: Hàm số ![]() liên tục trên mỗi khoảng
liên tục trên mỗi khoảng ![]() và
và ![]() nhưng gián đoạn tại
nhưng gián đoạn tại ![]()
Bài tập 6: Tìm ![]() để hàm số liên tục trên tập xác định của chúng:
để hàm số liên tục trên tập xác định của chúng:
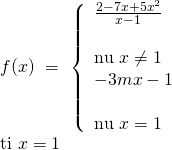
Hướng dẫn giải:
– Tập xác định: ![]()
– Nếu ![]() , thì hàm số
, thì hàm số ![]() .
.
Đây là hàm phân thức hữu tỉ có tập xác định là ![]() .
.
Vậy nó liên tục trên mỗi khoảng ![]() và
và ![]()
– Nếu ![]()
![]()
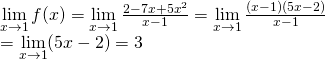
Do hàm số ![]() không liên tục tại
không liên tục tại ![]() nên
nên ![]() .
.
– Vậy: Giá trị ![]() cần tìm là
cần tìm là ![]()
Bài tập 7: Xét tính liên tục của hàm số trên tập xác định của chúng: 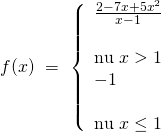
Hướng dẫn giải:
– Tập xác định: ![]()
– Nếu ![]() , thì hàm số
, thì hàm số ![]() .
.
Đây là hàm phân thức hữu tỉ có tập xác định là ![]() .
.
Vậy nó liên tục trên khoảng ![]() .
.
– Nếu ![]() , thì hàm số
, thì hàm số ![]() .
.
Đây là hàm đa thứccó tập xác định là ![]() .
.
Vậy nó liên tục trên mỗi khoảng ![]() . – Nếu
. – Nếu ![]()
![]()
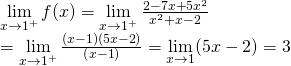
![]()
Do: ![]() nên hàm số
nên hàm số ![]() gián đoạn tại
gián đoạn tại ![]()
– Vậy: Hàm số ![]() liên tục trên
liên tục trên ![]() và gián đoạn tại
và gián đoạn tại ![]() .
.
Bài tập 8: Tìm ![]() để hàm số liên tục trên tập xác định của chúng:
để hàm số liên tục trên tập xác định của chúng: 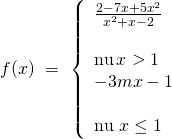
Hướng dẫn giải:
– Tập xác định: ![]()
– Nếu ![]() , thì hàm số
, thì hàm số ![]() .
.
Đây là hàm phân thức hữu tỉ có tập xác định là ![]() .
.
Vậy nó liên tục trên khoảng ![]() .
.
– Nếu ![]() , thì hàm số
, thì hàm số ![]() .
.
Đây là hàm đa thứccó tập xác định là ![]() .
.
Vậy nó liên tục trên mỗi khoảng ![]() .
.
– Nếu ![]()
![]()
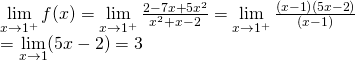
![]() .
.
Để hàm số ![]() gián đoạn tại
gián đoạn tại ![]() khi
khi ![]() .
.
– Vậy: Giá trị ![]() cần tìm là
cần tìm là ![]() .
.
Bài tập 9: Chứng minh phương trình ![]() có ba nghiệm trong khoảng
có ba nghiệm trong khoảng ![]() .
.
Hướng dẫn giải:
– Xét hàm số ![]() liên tục trên R nên
liên tục trên R nên ![]() liên tục trên mọi đoạn.
liên tục trên mọi đoạn.
– Ta có: ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Suy ra phương trình có nghiệm trong mỗi khoảng
. Suy ra phương trình có nghiệm trong mỗi khoảng ![]() ,
, ![]() ,
, ![]() .
.
– Vậy: Phương trìn có ba nghiệm trên khoảng ![]()
Bài tập 10: Chứng minh rằng phương trình: ![]() luôn có nghiệm
luôn có nghiệm ![]() với
với ![]() và
và ![]() .
.
Hướng dẫn giải:
– Xét hàm số ![]() liên tục trên
liên tục trên ![]() .
.
Ta có: ![]() ,
, ![]()
Do đó: ![]()
Như thế:
– Nếu ![]() hay
hay ![]() phương trình
phương trình ![]() hiển nhiên có nghiệm thuộc
hiển nhiên có nghiệm thuộc ![]() .
.
– Nếu ![]() và
và ![]() ta thấy
ta thấy ![]() .
.
Vậy: Phương trình ![]() có nghiệm trên
có nghiệm trên ![]() .
.
Bài tập 11: Với mọi ![]() , chứng minh phương trình:
, chứng minh phương trình: ![]() luôn luôn có nghiệm.
luôn luôn có nghiệm.
Hướng dẫn giải:
– Xét hàm số ![]() liên tục trên
liên tục trên ![]() .
.
![]() ,
, ![]() ,
, ![]()
Giả sử ![]() (tương tự các trường hợp sau)
(tương tự các trường hợp sau)
– Nếu ![]() hoặc
hoặc ![]() hoặc
hoặc ![]() ta có
ta có ![]() do đó
do đó ![]() là một nghiệm của phương trình.
là một nghiệm của phương trình.
– Nếu ![]() . Ít nhất có một trong hai trường hợp xảy ra:
. Ít nhất có một trong hai trường hợp xảy ra:
+Với ![]()
Suy ra phương trình có nghiệm trên đoạn ![]()
+Với ![]()
Suy ra phương trình có nghiệm trên đoạn ![]() .
.
Bài tập 12: Chứng minh rằng nếu ![]() thì phương trình
thì phương trình ![]() có ít nhất một nghiệm trong khoảng
có ít nhất một nghiệm trong khoảng ![]() với
với ![]()
Hướng dẫn giải:
– Xét hàm số ![]()
Đặt ![]() . Khi đó ta có:
. Khi đó ta có: ![]() có ít nhất một nghiệm
có ít nhất một nghiệm ![]() .
.
– Nếu ![]() . Ta có:
. Ta có: ![]() . Vậy phương trình
. Vậy phương trình ![]() có nghiệm
có nghiệm ![]() .
.
– Nếu ![]() , lúc đó phương trình có nghiệm
, lúc đó phương trình có nghiệm ![]() ,
, ![]() có nghĩa
có nghĩa ![]() .
.
– Nếu ![]() . Ta có:
. Ta có: ![]()
+Với ![]() phương trình
phương trình ![]() có vô số nghiệm nên tất nhiên sẽ có một nghiệm thuộc
có vô số nghiệm nên tất nhiên sẽ có một nghiệm thuộc ![]() .
.
+Với ![]() .
.
– Tóm lại: ![]() thỏa mãn
thỏa mãn ![]() thì phương trình
thì phương trình ![]() có ít nhất một nghiệm
có ít nhất một nghiệm ![]() , tức là
, tức là ![]() thì phương trình
thì phương trình ![]() có ít nhất một nghiệm trong khoảng
có ít nhất một nghiệm trong khoảng ![]() với
với ![]() .
.
Sotayhoctap chúc các bạn học tốt!




