Bài viết xét tính chẵn lẻ của hàm số bao gồm: cách xét tính chẵn lẻ của hàm số, bài tập xét tính chẵn lẻ của hàm số…
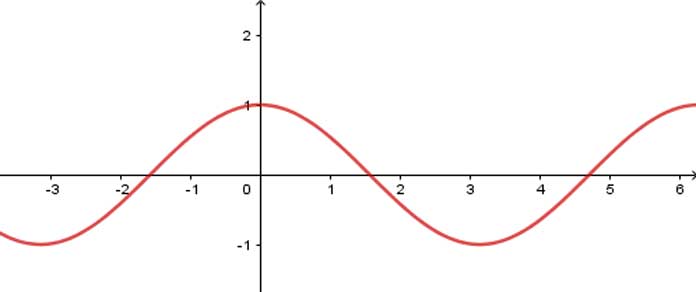
Khái niệm hàm số chẵn, hàm số lẻ
Cho hàm số ![]() có tập xác định D.
có tập xác định D.
Hàm số ![]() được gọi là hàm số chẵn nếu với
được gọi là hàm số chẵn nếu với ![]() thì
thì ![]() và
và ![]() .
.
Hàm số ![]() được gọi là hàm số lẻ nếu với
được gọi là hàm số lẻ nếu với ![]() thì
thì ![]() và
và ![]()
Chú ý: Một hàm số có thể không chẵn cũng không lẻ.
Đồ thị của hàm số chẵn, hàm số lẻ
Đồ thị của hàm số chẵn nhận trục tung làm trục đối xứng.
Đồ thị của hàm số lẻ nhận gốc toạ độ làm tâm đối xứng.
Cách xét tính chẵn lẻ của hàm số
Cho hàm số ![]() xác định trên
xác định trên ![]()
![]() là hàm số chẵn
là hàm số chẵn ![]()
![]() là hàm số lẻ
là hàm số lẻ ![]()
Các bước xét tính chẵn, lẻ của hàm số:
Bước 1. Tìm tập xác định ![]() của hàm số.
của hàm số.
Bước 2. Kiểm tra:
+ Nếu ![]() thì chuyển qua bước 3.
thì chuyển qua bước 3.
+ Nếu tồn tại ![]() mà
mà ![]() thì kết luận hàm không chẵn cũng không lẻ.
thì kết luận hàm không chẵn cũng không lẻ.
Bước 3. Xác định ![]() và so sánh với
và so sánh với ![]()
+ Nếu ![]() thì kết luận hàm số là chẵn.
thì kết luận hàm số là chẵn.
+ Nếu ![]() thì kết luận hàm số là lẻ.
thì kết luận hàm số là lẻ.
Bài tập xét tính chẵn lẻ của hàm số
Ví dụ 1. Xét tính chẵn, lẻ của các hàm số sau:
a) ![]()
b) ![]()
c) ![]()
d) ![]()
Giải
a) Tập xác định của hàm số: ![]()
Với mọi ![]() ta có
ta có ![]() và
và ![]()
Do đó ![]() là hàm số lẻ.
là hàm số lẻ.
b) Tập xác định của hàm số: ![]()
Với mọi ![]() ta có
ta có ![]() và
và 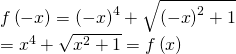
Do đó ![]() là hàm số chẵn.
là hàm số chẵn.
c) Điều kiện xác định: ![]()
Suy ra tập xác định của hàm số là: ![]()
Với mọi ![]() ta có
ta có ![]() và
và ![]()
Do đó ![]() là hàm số chẵn.
là hàm số chẵn.
d) Điều kiện xác định:
![]()
Suy ra tập xác định của hàm số là: ![]()
Ta có ![]() nhưng
nhưng ![]()
Vậy hàm số ![]() không chẵn và không lẻ.
không chẵn và không lẻ.
Ví dụ 2. Xét tính chẵn, lẻ của các hàm số sau:
a) ![]()
b) ![]()
c) ![]()
d) 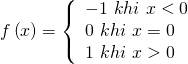
Giải
a) Tập xác định của hàm số: ![]()
Ta có
![]()
Vậy hàm số không chẵn và không lẻ.
b) Tập xác định của hàm số: ![]()
Với mọi ![]() ta có
ta có ![]() và
và ![]()
Suy ra ![]()
Do đó ![]() là hàm số chẵn.
là hàm số chẵn.
c) Ta có ![]()
Suy ra tập xác định của hàm số là: ![]() .
.
Mặt khác ![]() do đó
do đó 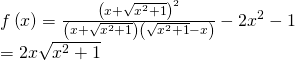
Với mọi ![]() ta có
ta có ![]() và
và 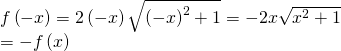
Do đó ![]() là hàm số lẻ.
là hàm số lẻ.
d) Tập xác định của hàm số: ![]()
Dễ thấy với mọi ![]() ta có
ta có ![]()
Với mọi ![]() ta có
ta có ![]() suy ra
suy ra ![]() ,
, ![]()
Với mọi ![]() ta có
ta có ![]() suy ra
suy ra ![]()
Và ![]()
Do đó với mọi ![]() ta có
ta có ![]()
Vậy hàm số 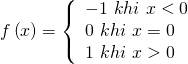 là hàm số lẻ.
là hàm số lẻ.
Ví dụ 3. Tìm ![]() để hàm số
để hàm số ![]() là hàm số chẵn.
là hàm số chẵn.
Điều kiện xác định: ![]()
Giả sử hàm số ![]() là hàm số chẵn suy ra
là hàm số chẵn suy ra ![]() với mọi x thỏa mãn điều kiện
với mọi x thỏa mãn điều kiện ![]()
Ta có![]()
Suy ra 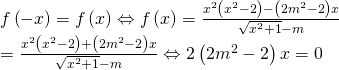 với mọi
với mọi ![]() thỏa mãn điều kiện xác định
thỏa mãn điều kiện xác định ![]() .
.
+ Với ![]() ta có hàm số là
ta có hàm số là ![]()
Điều kiện xác định: ![]()
Suy ra tập xác định của hàm số là: ![]()
Dễ thấy với mọi ![]() ta có
ta có ![]() và
và ![]()
Do đó ![]() là hàm số chẵn.
là hàm số chẵn.
+ Với ![]() ta có hàm số là
ta có hàm số là ![]()
Tập xác định của hàm số ![]()
Dễ thấy với mọi ![]() ta có
ta có ![]() và
và ![]()
Do đó ![]() là hàm số chẵn.
là hàm số chẵn.
Vậy ![]() là giá trị cần tìm.
là giá trị cần tìm.
Sotayhoctap chúc các bạn học tốt!




