Bài viết định lý viet bao gồm: định lý viet đảo, định lý viet thuận, bài tập định lý viet, định lý viet bậc 3, chuyên đề phương trình bậc hai và định lý viet, định lý viet và ứng dụng…
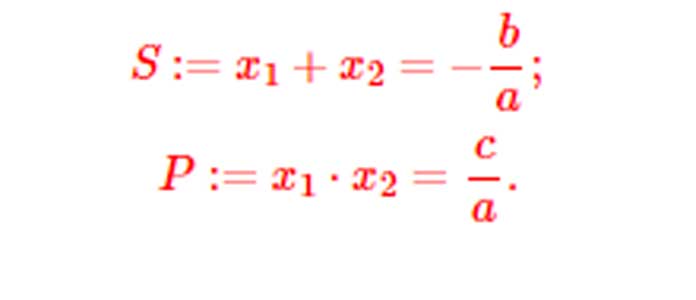
Định lý Viet
Định lý Viet thuận
Nếu phương trình bậc hai có dạng:
![]()
có 2 nghiệm phân biệt thì:
![]()
Định lý Viet đảo
Nếu ta có hai số u, v có u + v = S và u.v = P thì u và v là nghiệm của phương trình :
![]()
Ví dụ bài tập định lý viet
Bài 1: Tìm tổng và tích của các nghiệm phương trình sau: ![]()
Hướng dẫn: Đầu tiên ta tính ![]()
Ta có: ![]()
![]()
Bài 2: Tìm tổng và tích của các nghiệm phương trình sau:![]()
Hướng dẫn:
Với bài toán này, ta nhận thấy hệ số a và c trái dấu, như đã học ở bài trước, pt này chắc chắn có 2 nghiệm phân biệt.
Vậy: ![]()
![]()
Bài 3:Tìm tổng và tích của các nghiệm phương trình sau: ![]()
Hướng dẫn: Đầu tiên ta tính ![]()
Vậy ![]()
![]()
Bài 4: Tìm hai số biết tổng của chúng là 5 và tích của chúng là 6
Hướng dẫn: Gọi hai số đó là ![]() và
và ![]()
![]()
Lại có ![]()
Vậy 2 số cần tìm là nghiệm của phương trình ![]() hay
hay ![]()
![]() hoặc
hoặc ![]()
Bài 5: Tìm hai số biết hiệu của chúng là 11 và tích của chúng là 60
Hướng dẫn: Gọi hai số cần tim là a, b
Ta có ![]()
Thế ![]() vào phương trình tích, ta được
vào phương trình tích, ta được ![]()
![]() hoặc
hoặc ![]()
![]()
![]()
Bài 6: Định ![]() để phương trình
để phương trình ![]() có hai nghiệm phân biệt
có hai nghiệm phân biệt ![]() thoả mãn đẳng thức
thoả mãn đẳng thức ![]()
Hướng dẫn:
Ta có ![]() Phương trình có hai nghiệm phân biệt khi
Phương trình có hai nghiệm phân biệt khi ![]() Khi đó, theo định lý Vi-et ta có
Khi đó, theo định lý Vi-et ta có
![]()
Đẳng thức đã cho tương đương
![]()
Định lý viet bậc 3
Cho phương trình:
![]()
Định lý Viet thuận
Nếu phương trình có 3 nghiệm x1, x2, x3 thì ta có:
![Rendered by QuickLaTeX.com \[\left\{ \begin{array}{l} {x_1} + {x_2} + {x_3} = \frac{{ - b}}{a}\\ {x_1}{x_2} + {x_2}{x_3} + {x_3}{x_1} = \frac{c}{a}\\ {x_1}{x_2}{x_3} = \frac{{ - d}}{a} \end{array} \right.\]](https://sotayhoctap.com/wp-content/ql-cache/quicklatex.com-e020d17f33327936da9c15ad608c9073_l3.png)
Định lý Viet đảo
Nếu 3 số x, y, z thỏa mãn:
![Rendered by QuickLaTeX.com \[\left\{ \begin{array}{l} x + y + z = a\\ xy + yz + xz = b\\ xyz = c \end{array} \right.\]](https://sotayhoctap.com/wp-content/ql-cache/quicklatex.com-e61d0423da24560b1dfc3e1d8d6f36ea_l3.png)
Thì x, y,z là 3 nghiệm của phương trình:
![]()
Các dạng toán ứng dụng định lý Viet
Tìm hệ thức liên hệ giữa 2 nghiệm của phương trình sao cho chúng không phụ huộc vào tham số
Phương pháp:
Để làm các bài toán loại này, ta làm lần lượt theo các bước sau:
– Đặt điều kiện cho tham số để phương trình đã cho có hai nghiệm ![]() và
và ![]() (thường là
(thường là ![]() và
và ![]() )
)
– Áp dụng hệ thức VI-ÉT viết ![]() và
và ![]() theo tham số
theo tham số
– Dùng quy tắc cộng hoặc thế để tính tham số theo ![]() và
và ![]() . Từ đó đưa ra hệ thức liên hệ giữa các nghiệm
. Từ đó đưa ra hệ thức liên hệ giữa các nghiệm ![]() và
và ![]() .
.
Bài 1:
Cho phương trình: ![]() có 2 nghiệm
có 2 nghiệm ![]() . Lập hệ thức liên hệ giữa
. Lập hệ thức liên hệ giữa ![]() sao cho chúng không phụ thuộc vào
sao cho chúng không phụ thuộc vào ![]() .
.
Giải:
Để phương trình trên có 2 nghiệm ![]() và
và ![]() thì :
thì :
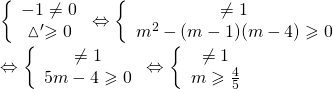
Theo hệ thức VI-ÉT ta có :
![]()
Rút ![]() từ (1) ta có :
từ (1) ta có :
![]() (3)
(3)
Rút ![]() từ (2) ta có :
từ (2) ta có :
![]() (4)
(4)
Đồng nhất các vế của (3) và (4) ta có:
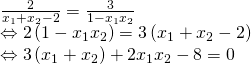
Bài 2:
Gọi ![]() ,
,![]() là nghiệm của phương trình :
là nghiệm của phương trình : ![]() .
.
Chứng minh rằng biểu thức ![]() không phụ thuộc giá trị của
không phụ thuộc giá trị của ![]() .
.
Giải:
Để phương trình trên có 2 nghiệm ![]() và
và ![]() thì :
thì :
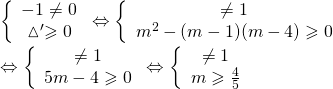
Theo hệ thức VI-ÉT ta có :
![]() thay vào
thay vào ![]() ta có:
ta có:
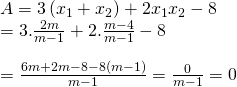
Vậy ![]() với mọi
với mọi ![]() và
và ![]() . Do đó biểu thức
. Do đó biểu thức ![]() không phụ thuộc vào
không phụ thuộc vào ![]()
Nhận xét:
– Lưu ý điều kiện cho tham số để phương trình đã cho có 2 nghiệm
– Sau đó dựa vào hệ thức VI-ÉT rút tham số theo tổng nghiệm, theo tích nghiệm sau đó đồng nhất các vế ta sẽ được một biểu thức chứa nghiệm không phụ thuộc vào tham số.
Bài 3:
Cho phương trình : ![]() có 2 nghiệm
có 2 nghiệm ![]() và
và ![]() . Hãy lập hệ thức liên hệ giữa
. Hãy lập hệ thức liên hệ giữa ![]() sao cho
sao cho ![]() độc lập đối với
độc lập đối với ![]() .
.
Hướng dẫn:
Dễ thấy ![]()
do đó phương trình đã cho luôn có 2 nghiệm phân biệt ![]() và
và ![]()
Theo hệ thức VI-ÉT ta có:
![]()
Từ (1) và (2) ta có:
![]()
Bài 4:
Cho phương trình : ![]() .
.
Tìm hệ thức liên hệ giữa ![]() và
và ![]() sao cho chúng không phụ thuộc vào
sao cho chúng không phụ thuộc vào ![]() .
.
Hướng dẫn:
Dễ thấy ![]() do đó phương trình đã cho luôn có 2 nghiệm phân biệt
do đó phương trình đã cho luôn có 2 nghiệm phân biệt ![]() và
và ![]()
Theo hệ thức VI-ÉT ta có
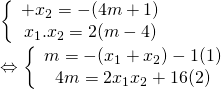
Từ (1) và (2) ta có:
![]()
Tìm giá trị tham số của phương trình thỏa mãn biểu thức chứa nghiệm đã cho
Phương pháp:
Đối với các bài toán dạng này, ta làm như sau:
– Đặt điều kiện cho tham số để phương trình đã cho có hai nghiệm ![]() và
và ![]() (thường là
(thường là ![]() và
và ![]() )
)
– Từ biểu thức nghiệm đã cho, áp dụng hệ thức VI-ÉT để giải phương trình (có ẩn là tham số).
– Đối chiếu với điều kiện xác định của tham số để xác định giá trị cần tìm.
Bài 1:
Cho phương trình : ![]()
Tìm giá trị của tham số m để 2 nghiệm ![]() và
và ![]() thoả mãn hệ thức :
thoả mãn hệ thức : ![]()
Giải:
Điều kiện để phương trình có 2 nghiệm ![]() và
và ![]() là :
là :
![Rendered by QuickLaTeX.com \left\{ \begin{array} m \ne 0 \\ \Delta ' = {\left[ {3\left( {m - 21} \right)} \right]^2} - 9(m - 3)m \geqslant 0 \\ \end{array} \right. \\ \Leftrightarrow \left\{ \begin{array} m \ne 0 \\ \Delta ' = 9\left( {{m^2} - 2m + 1} \right) - 9{m^2} + 27 \geqslant 0 \\ \end{array} \right.\\ \Leftrightarrow \left\{ \begin{array} m \ne 0 \\ \Delta ' = 9\left( {m - 1} \right) \geqslant 0 \\ \end{array} \right. \Leftrightarrow \left\{ \begin{array} m \ne 0 \\ m \geqslant - 1 \\ \end{array} \right.](https://sotayhoctap.com/wp-content/ql-cache/quicklatex.com-bcf6aff04b4b35a22f2baa369e646efe_l3.png)
Theo hệ thức VI-ÉT ta có: 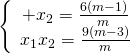
Và từ giả thiết: ![]() . Suy ra:
. Suy ra:
![]()
(thoả mãn điều kiện xác định )
Vậy với ![]() thì phương trình đã cho có 2 nghiệm
thì phương trình đã cho có 2 nghiệm ![]() và
và ![]() thoả mãn hệ thức :
thoả mãn hệ thức : ![]()
Bài 2:
Cho phương trình : ![]()
Tìm ![]() để 2 nghiệm
để 2 nghiệm ![]() và
và ![]() thoả mãn hệ thức :
thoả mãn hệ thức : ![]()
Giải:
Điều kiện để phương trình có 2 nghiệm ![]() là :
là :
![]()
![]()
![]()
Theo hệ thức VI-ÉT ta có: ![]()
và từ giả thiết . Suy ra
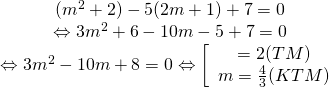
Vậy với ![]() thì phương trình có 2 nghiệm và thoả mãn hệ thức :
thì phương trình có 2 nghiệm và thoả mãn hệ thức :
Bài 3:
Cho phương trình : ![]()
Tìm ![]() để 2 nghiệm
để 2 nghiệm ![]() và
và ![]() thoả mãn hệ thức :
thoả mãn hệ thức : ![]()
Hướng dẫn:
– ĐKX Đ: ![]()
-Theo VI-ÉT: ![]()
– Từ Suy ra: ![]() (2)
(2)
– Thế (1) vào (2) ta đưa được về phương trình sau:
![]()
Tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của biểu thức nghiệm
Phương pháp:
Áp dụng tính chất sau về bất đẳng thức: trong mọi trường hợp nếu ta luôn phân tích được:
![]() (trong đó
(trong đó ![]() là các biểu thức không âm ;
là các biểu thức không âm ; ![]() là hằng số) (*)
là hằng số) (*)
Thì ta thấy : ![]() (v ì
(v ì ![]() )
) ![]()
![]() (v ì
(v ì![]() )
) ![]()
Bài 1:
Cho phương trình : ![]()
Gọi ![]() và
và ![]() là các nghiệm của phương trình. Tìm
là các nghiệm của phương trình. Tìm ![]() để:
để: ![]() có giá trị nhỏ nhất.
có giá trị nhỏ nhất.
Giải:
Theo VI-ÉT: ![]()
Theo đề bài : ![]()
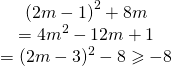
Suy ra: ![]() hay
hay ![]()
Bài 2:
Cho phương trình : ![]()
Gọi ![]() và
và ![]() là các nghiệm của phương trình. Tìm giá trị nhỏ nhất và giá trị lớn nhất của biểu thức sau:
là các nghiệm của phương trình. Tìm giá trị nhỏ nhất và giá trị lớn nhất của biểu thức sau:
![]()
Giải:
Ta có: Theo hệ thức VI-ÉT thì :
![]()
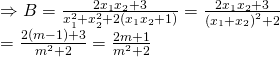
Thêm bớt để đưa về dạng như phần (*) đã hướng dẫn
Ta biến đổi B như sau:
![]()
Vì ![]()
Vậy ![]() m = 1
m = 1
Với cách thêm bớt khác ta lại có:
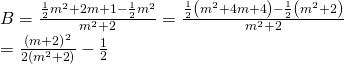
Vì ![]()
Vậy ![]()
Sotayhoctap chúc các bạn học tốt!




