Tổng hợp công thức đạo hàm lượng giác, công thức đạo hàm lượng giác ngược, công thức đạo hàm lượng giác có mũ…

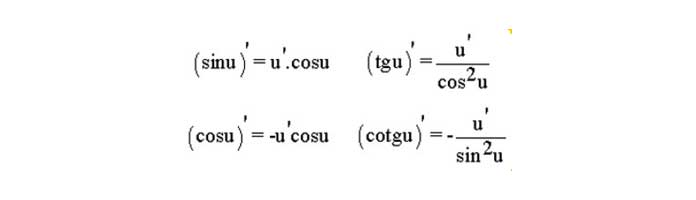
Công thức đạo hàm lượng giác

Đạo hàm của hàm số y=sinx

Hàm số $y=sin x$ có đạo hàm tại mọi $x \in \mathbb{R}$ và $\left( {\sin x} \right)' = \cos x.$

Nếu $y=sin u$ và $u=u(x)$ thì $(sin u)'=u'. \cos u.$

Đạo hàm của hàm số y=cosx

Hàm số $y=\cos x$ có đạo hàm tại mọi $x \in \mathbb{R}$ và $\left( {\cos x} \right)' =-\sin x.$

Nếu $y=\cos u$ và $u=u(x)$ thì $(cos u)'=-u'. \sin u.$

Đạo hàm của hàm số y=tanx

Hàm số $y=\tan x$ có đạo hàm tại mọi $x \ne \frac{\pi }{2} + k\pi ,k \in \mathbb{R}$ và $\left( {\tan x} \right)' = \frac{1}{{{{\cos }^2}x}}.$

Nếu $y=tan u$ và $u=u(x)$ thì $\left( {\tan u} \right)' = \frac{{u'}}{{{{\cos }^2}u}}.$

Đạo hàm của hàm số y=cotx

Hàm số $y=\cot x$ có đạo hàm tại mọi $x \ne k\pi ,k \in \mathbb{R}$ và $\left( {\cot x} \right)' = - \frac{1}{{{{\sin }^2}x}}.$

Nếu $y=\cot u$ và $u=u(x)$ thì $\left( {\cot x} \right)' = - \frac{{u'}}{{{{\sin }^2}u}}$ .

Công thức đạo hàm lượng giác ngược

(Hàm lượng giác ngược có 2 cách viết, ví dụ hàm số lượng giác ngược của $\sin(x)$ có thể viết thành là $sin^{-1}(x)$ hoặc $\arcsin(x)$ , mình chọn cách viết thứ hai.)

Đạo hàm của $\arcsin$ : $y = \arcsin(x) \Rightarrow y' = \frac{1}{\sqrt{1 - x^2}}$

Đạo hàm của $\arccos$ : $y = \arccos(x) \Rightarrow y' = -\frac{1}{\sqrt{1 - x^2}}$

Đạo hàm của $\arctan$ : $y = \arctan(x) \Rightarrow y' = \frac{1}{1 + x^2}$

Đạo hàm của $\text{arccot}$ : $y = \text{arccot}(x) \Rightarrow y' = -\frac{1}{1 + x^2}$

Đạo hàm của $\text{arcsec}$ : $y = \text{arcsec}(x) \Rightarrow y' = \frac{1}{|x| \sqrt{x^2 - 1}}$

Đạo hàm của $\text{arccsc}$ : $y = \text{arccsc}(x) \Rightarrow y' = -\frac{1}{|x| \sqrt{x^2 - 1}}$

Công thức đạo hàm lượng giác có mũ

$\begin{array}{l} {(Sinax)^n} = {a^n}.Sin(ax + n.\frac{\Pi }{2})\\ {(Cosax)^n} = {a^n}.Cos(ax + n.\frac{\Pi }{2}) \end{array}$

Đạo hàm của hàm hyperbolic

Đạo hàm của $\sinh$ : $y = \sinh(x) \Rightarrow y' = \cosh(x)$

Đạo hàm của $\cosh$ : $y = \cosh(x) \Rightarrow y' = \sinh(x)$

Đạo hàm của $\tanh$ : $y = \tanh(x) \Rightarrow y' = \text{sech}^2(x) = 1 - \tanh^2(x) \\= \frac{1}{\cosh^2(x)}$

Đạo hàm của $\coth$ : $y = \coth(x) \Rightarrow y' = -\text{csch}^2(x) = 1 - \coth^2(x) \\= -\frac{1}{\sinh^2(x)}$

Đạo hàm của $\text{sech}$ : $y = \text{sech}(x) \Rightarrow y' = -\tanh(x) \text{ sech}(x)$

Đạo hàm của $\text{csch}$ : $y = \text{csch}(x) \Rightarrow y' = -\coth(x) \text{ csch}(x)$

Đạo hàm của hàm hyperbolic ngược

Đạo hàm của $\text{arsinh}$ : $y = \text{arsinh}(x) \Rightarrow y' = \frac{1}{\sqrt{x^2 + 1}}$

Đạo hàm của $\text{arcosh}$ : $y = \text{arcosh}(x) \Rightarrow y' = \frac{1}{\sqrt{x^2 - 1}}$

Đạo hàm của $\text{artanh}$ : $y = \text{artanh}(x) \Rightarrow y' = \frac{1}{1 - x^2}$

Đạo hàm của $\text{arcoth}$ : $y = \text{arcoth}(x) \Rightarrow y' = \frac{1}{1 - x^2}$

Đạo hàm của $\text{arsech}$ : $y = \text{arsech}(x) \Rightarrow y' = -\frac{1}{x \sqrt{1 - x^2}}$

Đạo hàm của $\text{arcsch}$ : $y = \text{arcsch}(x) \Rightarrow y' = -\frac{1}{|x| \sqrt{1 + x^2}}$

Chú ý khi áp dụng công thức đạo hàm của các hàm lượng giác các bạn nên quan tâm luôn tới giá trị của $x$ , ví dụ đạo hàm của $\arcsin(x)$ sẽ không xác định khi $x = -1$ và $x = 1$ , do đó phải có điều kiện $x \neq -1$ và $x \neq 1$ .

Ví dụ công thức đạo hàm lượng giác

Ví dụ 1:
Tìm đạo hàm của các hàm số sau:

a) $y = \sin \left( {\frac{\pi }{2} - x} \right).$

b) $y = \sin \sqrt {x + 10} .$

c) $y = \sin \left( {\frac{1}{{x - 2}}} \right).$

Lời giải:
a) $y = \sin \left( {\frac{\pi }{2} - x} \right)$ $\Rightarrow y' = \left( {\frac{\pi }{2} - x} \right)'.\cos \left( {\frac{\pi }{2} - x} \right)$ $= - \cos \left( {\frac{\pi }{2} - x} \right).$

b) $y = \sin \sqrt {x + 10}$ $\Rightarrow y' = \left( {\sqrt {x + 10} } \right)'.\cos \sqrt {x + 10}$ $= \frac{1}{{2\sqrt {x + 10} }}.\cos \sqrt {x + 10} .$

c) $y = \sin \left( {\frac{1}{{x - 2}}} \right)$ $\Rightarrow y' = \left( {\frac{1}{{x - 2}}} \right)'.\cos \left( {\frac{1}{{x - 2}}} \right)$ $= \frac{{ - 1}}{{{{\left( {x - 2} \right)}^2}}}.\cos \left( {\frac{1}{{x - 2}}} \right).$

Ví dụ 2:
Tìm đạo hàm của các hàm số sau:

a) $y = \cos \left( {{x^3} - x} \right).$

b) $y = \cos \sqrt {{x^2} - 8} .$

c) $y = \cos \left( {\frac{x}{{x + 4}}} \right).$

Lời giải:
a) $y = \cos \left( {{x^3} - x} \right)$ $\Rightarrow y' = - \left( {{x^3} - x} \right)'.\sin \left( {{x^3} - x} \right)$ $= - \left( {3{x^3} - 1} \right).\sin \left( {{x^3} - x} \right).$

b) $y = \cos \sqrt {{x^2} - 8}$ $\Rightarrow y' = - \left( {\sqrt {{x^2} - 8} } \right)'.\sin \sqrt {x + 10}$ $= \frac{x}{{\sqrt {{x^2} - 8} }}.\sin \sqrt {{x^2} - 8} .$

c) $y = \cos \left( {\frac{x}{{x + 4}}} \right)$ $\Rightarrow y' = \left( {\frac{x}{{x + 4}}} \right)'.\sin \left( {\frac{1}{{x - 2}}} \right)$ $= \frac{4}{{{{\left( {x + 4} \right)}^2}}}.\sin \left( {\frac{x}{{x + 4}}} \right).$

Ví dụ 3:
Tính đạo hàm của các hàm số sau:

a) $y = \tan \left( {{x^5} - 5x} \right)$ .

b) $y = \tan \sqrt {{x^4} + 1}$ .

Lời giải:
a) $y = \tan \left( {{x^5} - 5x} \right)$ $\Rightarrow y' = \frac{{({x^5} - 5x)'}}{{{{\cos }^2}\left( {{x^5} - 5x} \right)}} = \frac{{5{x^4} - 5}}{{{{\cos }^2}\left( {{x^5} - 5x} \right)}}$ .

b) $y = \tan \sqrt {{x^4} + 1}$ $\Rightarrow y' = \frac{{\left( {\sqrt {{x^4} + 1} } \right)}}{{{{\cos }^2}\left( {\sqrt {{x^4} + 1} } \right)}} = \frac{{2{x^3}}}{{\sqrt {{x^4} + 1} .{{\cos }^2}\left( {\sqrt {{x^4} + 1} } \right)}}$ .

Ví dụ 4:
Tính đạo hàm của các hàm số sau:

a) $y = \cot \left( {7{x^3} - 6x} \right)$ .

b) $y = {\cot ^4}\left( {5x + 1} \right)$ .

Lời giải:
a) $y = \cot \left( {7{x^3} - 6x} \right)$ $\Rightarrow y' = \frac{{(7{x^3} - 6x)'}}{{{{\sin }^2}\left( {7{x^3} - 6x} \right)}} = - \frac{{21{x^2} - 6}}{{{{\sin }^2}\left( {7{x^3} - 6x} \right)}}$ .

b) $y = {\cot ^4}\left( {5x + 1} \right)$ $\Rightarrow y' = 4{\cot ^3}\left( {5x + 1} \right).\left[ {\cot \left( {5x + 1} \right)} \right]'$

$= 4{\cot ^3}\left( {5x + 1} \right).\left( {\frac{{ - 5}}{{{{\sin }^2}\left( {5x + 1} \right)}}} \right)$ $= \frac{{ - 20{{\cot }^3}\left( {5x + 1} \right)}}{{{{\sin }^2}\left( {5x + 1} \right)}}$ .

Download bảng công thức đạo hàm đầy đủ pdf

Các bạn có thể tải bảng công thức đạo hàm đầy đủ pdf dưới đây để in ra tiện cho việc tra cứu và học tập.

Download

Trên đây là bài viết công thức đạo hàm lượng giác đầy đủ và ví dụ áp dụng, Sotayhoctap chúc các bạn học tốt!

5/5 - (1 bình chọn)

SỔ TAY HỌC TẬP | SOTAYHOCTAP.COM

Công thức đạo hàm lượng giác đầy đủ và ví dụ áp dụng

Công thức đạo hàm lượng giác

Đạo hàm của hàm số y=sinx

Đạo hàm của hàm số y=cosx

Đạo hàm của hàm số y=tanx

Đạo hàm của hàm số y=cotx

Công thức đạo hàm lượng giác ngược

Công thức đạo hàm lượng giác có mũ

Đạo hàm của hàm hyperbolic

Đạo hàm của hàm hyperbolic ngược

Ví dụ công thức đạo hàm lượng giác

Download bảng công thức đạo hàm đầy đủ pdf

Công thức đạo hàm lượng giác

Đạo hàm của hàm số y=sinx

Đạo hàm của hàm số y=cosx

Đạo hàm của hàm số y=tanx

Đạo hàm của hàm số y=cotx

Công thức đạo hàm lượng giác ngược

Công thức đạo hàm lượng giác có mũ

Đạo hàm của hàm hyperbolic

Đạo hàm của hàm hyperbolic ngược

Ví dụ công thức đạo hàm lượng giác

Download bảng công thức đạo hàm đầy đủ pdf

Related Posts

Chuyên đề số chính phương

Lược đồ Hoocne (Sơ đồ Hoocne) trong cách chia đa thức

Nhị thức Newton, cách khai triển và một số dạng bài tập áp dụng

Những hằng đẳng thức đáng nhớ, hằng đẳng thức mở rộng và dạng toán áp dụng

Hàm số liên tục và bài toán xét tính liên tục của hàm số

Cách tìm tập xác định của hàm số mũ và hàm số logarit