Bài viết cách tìm tập xác định của hàm số mũ và hàm số logarit, đây là dạng toán cơ bản trong chương trình Giải tích 12. Muốn giải được những bài toán liên quan đến hàm số mũ, logarit chính xác nhất thì bước đầu tiên luôn luôn phải tìm đó là tìm tập xác định của hàm số mũ.

Phương pháp tìm tập xác định của hàm số mũ và hàm số logarit
Tập xác định của hàm số ![]() là tập các giá trị
là tập các giá trị ![]() sao cho tồn tại
sao cho tồn tại ![]()
Tìm tập xác định của hàm số mũ
Hàm số mũ ![]() xác định khi:
xác định khi:
+ Nếu ![]() và
và ![]() xác định.
xác định.
+ Nếu ![]() thì
thì ![]()
+ Nếu ![]() thì
thì ![]() Hàm số
Hàm số ![]() xác định
xác định ![]()
![]()
Tìm tập xác định của hàm số logarit
Hàm số logarit ![]() xác định khi
xác định khi ![]() ,
, ![]() và
và ![]() xác định,
xác định, ![]()
Hàm số ![]() xác định
xác định ![]()
![]() Hàm số
Hàm số ![]() xác định
xác định ![]()
![]()
Trong trường hợp có mẫu số thì phải có điều kiện mẫu số xác định và khác ![]() , nếu có biểu thức chứa ẩn số trong dấu căn bậc chẵn, biểu thức phải xác định và không âm.
, nếu có biểu thức chứa ẩn số trong dấu căn bậc chẵn, biểu thức phải xác định và không âm.
Ví dụ tìm tập xác định của hàm số mũ và hàm số logarit
Ví dụ 1: Tìm tập xác định của hàm số ![]()
Lời giải:
Hàm số xác định khi ![]()
![]()
![]()
![]()
Vậy tập xác định ![]()
Ví dụ 2: Tìm tập xác định của hàm số:
a) ![]()
b) ![]()
Lời giải:
a) Hàm số xác định khi ![]()
![]()
![]() Vậy
Vậy ![]() b) Tương tự, ta có:
b) Tương tự, ta có: ![]()
Vậy ![]()
Ví dụ 3: Tìm tập xác định và tập giá trị của hàm số: ![]()
Lời giải:
Hàm số xác định khi: ![]()
![]()
![]()
![]()
Vậy tập xác định là ![]()
Ta có ![]() :
: ![]()
![]()
Vậy tập giá trị của hàm số là ![]()
Ví dụ 4: Tìm tập xác định của các hàm số:
a) ![]()
b) ![]()
c) ![]()
Lời giải:
a) Hàm số xác định khi 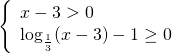
![]() Vậy
Vậy ![]() b) Lập điều kiện:
b) Lập điều kiện: 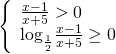
Giải hệ ta có ![]()
Vậy ![]()
c) Hàm số xác định khi 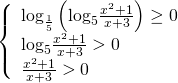
![]()
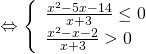
![]()
![]() Vậy tập xác định là
Vậy tập xác định là ![]() Ví dụ 5: Tìm tập xác định của các hàm số: a)
Ví dụ 5: Tìm tập xác định của các hàm số: a) ![]() b)
b) ![]() c)
c) ![]() Lời giải: a) Lập điều kiện
Lời giải: a) Lập điều kiện ![]()
Suy ra ![]()
b) 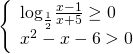
![]()
Suy ra ![]()
c) ![]()
Suy ra ![]()
Ví dụ 5: Tìm tập xác định của hàm số: ![]()
![]()
Lời giải:
Hàm số xác định khi: ![]()
![]()
![]() Tập xác định của hàm số là
Tập xác định của hàm số là ![]() Ví dụ 7: Tìm miền xác định của hàm số:
Ví dụ 7: Tìm miền xác định của hàm số: ![]() Lời giải: Hàm số xác định khi:
Lời giải: Hàm số xác định khi: ![]()
![]() Giải
Giải ![]() , ta có:
, ta có: ![]()
![]() hoặc
hoặc ![]()
![]()
![]() Suy ra
Suy ra ![]() Vậy
Vậy ![]() Ví dụ 8: Tìm tập xác định của hàm số:
Ví dụ 8: Tìm tập xác định của hàm số: ![]()
![]() Lời giải: Hàm số xác định khi:
Lời giải: Hàm số xác định khi: 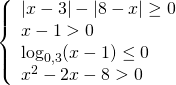
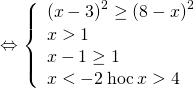
![]()
Vậy ![]()
Ví dụ 6: Tìm tập xác định của hàm số: ![]()
Lời giải:
Hàm số xác định khi:
![]()
![]()
![]()
![]()
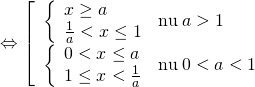 Vậy: + Với
Vậy: + Với ![]() :
: ![]()
+ Với ![]() :
: ![]() Ví dụ 10: Tìm các giá trị của m để hàm số
Ví dụ 10: Tìm các giá trị của m để hàm số ![]() xác định
xác định ![]() Lời giải: Hàm số xác định
Lời giải: Hàm số xác định ![]() khi
khi ![]()
![]()
![]()
![]()
Vì ![]() nên
nên ![]()
![]()
![]()
Với ![]() , hàm số đã cho xác định
, hàm số đã cho xác định ![]()
Ví dụ 7: Cho hàm số ![]()
a) Tìm tập xác định của hàm số khi ![]()
b) Tìm các giá trị của ![]() sao cho hàm số xác định
sao cho hàm số xác định ![]()
Lời giải:
a) Với ![]() ta có
ta có ![]() xác định khi
xác định khi 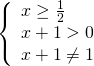
![]()
Vậy ![]()
b) Hàm số xác định với mọi ![]() khi và chỉ khi
khi và chỉ khi 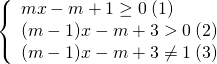
![]()
Giải bất phương trình, ta có:
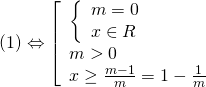
![]() có tập nghiệm là:
có tập nghiệm là:
+ Nếu ![]() thì
thì ![]()
+ Nếu ![]() thì
thì ![]()
Nếu ![]() thì
thì ![]() và
và ![]() đều thỏa mãn điều kiện.
đều thỏa mãn điều kiện.
Nếu ![]() thì
thì ![]() không thỏa
không thỏa ![]() Nếu
Nếu ![]() thì
thì ![]()
Vì ![]() ,
, ![]() nên
nên ![]() thỏa
thỏa ![]()
Với ![]() thì
thì ![]() thỏa
thỏa ![]()
Đáp số: ![]()
Sotayhoctap chúc các bạn học tốt!




