Góc giữa 2 vecto là gì? Cách xác định góc giữa 2 vecto, công thức tính góc giữa 2 vecto trong không gian OXYZ và các ví dụ về tính góc giữa 2 vectơ…
Định nghĩa góc giữa hai vecto
Cho hai vectơ ![]() và
và ![]() được mô tả như hình sau:
được mô tả như hình sau:
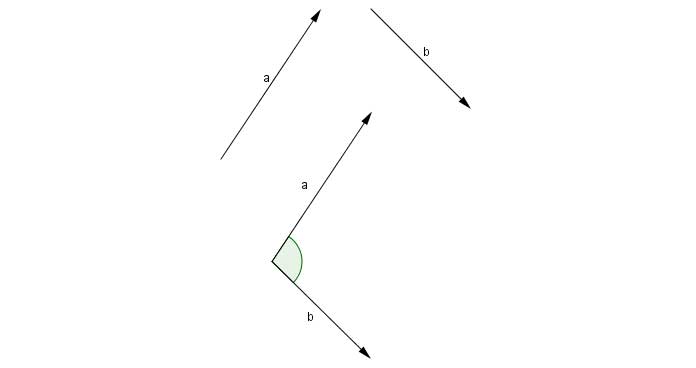
Số đo góc trên được gọi là số đo của góc giữa hai vectơ ![]() và
và ![]() .
.
Nếu số đo ấy bằng 90 độ, ta nói ![]() vuông góc với
vuông góc với ![]() .
.
Công thức tính góc giữa 2 vecto
Tính góc giữa 2 vecto
Tìm góc dựa vào giá trị cosin của nó. Bạn có thể dùng chức năng arccos hoặc cos-1 trong máy tính bỏ túi để tìm góc từ giá trị ![]() đã biết. Với một số kết quả thu được, có thể bạn sẽ tìm được góc dựa trên vòng tròn đơn vị. Tính góc giữa 2 vecto ta dựa vào công thức tích vô hướng của 2 vectơ:
đã biết. Với một số kết quả thu được, có thể bạn sẽ tìm được góc dựa trên vòng tròn đơn vị. Tính góc giữa 2 vecto ta dựa vào công thức tích vô hướng của 2 vectơ:
Cho hai vectơ ![]() . Khi đó:
. Khi đó:
![]()
![]()
Công thức tính góc giữa 2 vecto trong oxyz
![]()
![]() là 1 VTPT của (P)
là 1 VTPT của (P)
![]() là 1 VTPT của (Q)
là 1 VTPT của (Q)
![]()
![]()
Chú ý:
![]()
![]()
![]()
Bài tập ví dụ tính góc giữa hai vecto
Ví dụ 1: Tính cosin của góc giữa hai mặt phẳng
![]()
Giải:
(P) có 1 VTPT ![]()
(Q) có 1 VTPT ![]()
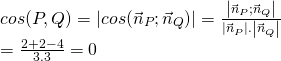
Vậy cos(P;Q) = 0
Ví dụ 2: Cho ![]()
Tìm m để
![]()
Giải:
(P) có 1 VTPT ![]()
(Q) có 1 VTPT ![]()
a)
![]()
![]()
![]()
b)
![]()
![]()
![]()
![]()
![]()
![]()
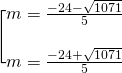
Ví dụ 3: Viết phương trình ![]() chứa OZ và tạo với (P)
chứa OZ và tạo với (P) ![]() một góc 600
một góc 600
Giải
Gọi ![]()
là 1 VTPT của ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
+ Nếu b = 0 thì a = 0 (vô lý)
+ Nếu ![]() thì chia 2 vế (1) cho b2 ta có
thì chia 2 vế (1) cho b2 ta có
![]()
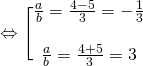
Trường hợp 1:
![]() , ta chọn a = -1, b = 3
, ta chọn a = -1, b = 3
![]()
![]() đi qua O(0;0;0) có 1 VTPT
đi qua O(0;0;0) có 1 VTPT ![]() nên có pt -x + 3y = 0
nên có pt -x + 3y = 0
Trường hợp 2:
![]() chọn
chọn ![]()
![]()
![]() đi qua O(0;0;0) có 1 VTPT
đi qua O(0;0;0) có 1 VTPT ![]() nên có phương trình 3x + y = 0
nên có phương trình 3x + y = 0
Vậy -x + 3y = 0, 3x + y = 0
Sotayhoctap chúc các bạn học tốt!




