Bảng công thức đạo hàm cơ bản bao gồm: các công thức tính đạo hàm, công thức đạo hàm lượng giác, công thức đạo hàm cấp cao, công thức đạo hàm logarit, công thức tính đạo hàm cấp cao…

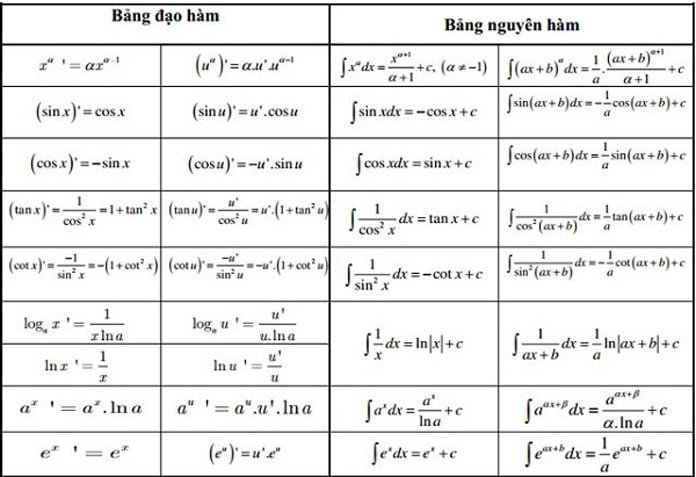
Các công thức đạo hàm cơ bản

Đạo hàm của một số hàm số thường gặp

Định lý 1: Hàm số $y = {x^n}(n \in \mathbb{N},n > 1$ ) có đạo hàm với mọi $x \in\mathbb{R}$ và: ${\left( {{x^n}} \right)'} = n{x^{n - 1}}.$

Nhận xét:

(c)’=0 (với c là hằng số).
(x)’=1.
Định lý 2: Hàm số $y= \sqrt x$ có đạo hàm với mọi x dương và: $\left( {\sqrt x } \right)' = \frac{1}{{2\sqrt x }}.$

Đạo hàm của tổng, hiệu, tích, thương

Định lý 3: Giả sử $u = u\left( x \right)$ và $v = v\left( x \right)$ là các hàm số có đạo hàm tại điểm x thuộc khoảng xác định. Ta có:

${\left( {u + v} \right)'} = {u'} + {v'}$
${\left( {u - v} \right)'} = {u'} - {v'}$
${\left( {u.v} \right)'} = {u'}.v + u.{v'}$
$\left ( \frac{u}{v} \right )'=\frac{u'v-uv'}{v^2},(v(x) \ne 0)$
Mở rộng:

$({u_1} + {u_2} + ... + {u_n})' = {u_1}' + {u_2}' + ... + {u_n}'.$
Hệ quả 1: Nếu k là một hằng số thì: $(ku)'=ku'.$

Hệ quả 2: ${\left( {\frac{1}{v}} \right)'} = - \frac{{ - v'}}{{{v^2}}}$ , $(v(x)\ne 0)$

$(u.v.{\rm{w}})' = u'.v.{\rm{w}} + u.v'.{\rm{w}} + u.v.{\rm{w}}'$

Đạo hàm với hàm hợp

Định lý: Cho hàm số $y=f(u)$ với $u=u(x)$ thì ta có: $y'_u=y'_u.u'_x.$

Hệ quả:

$({u^n}) = n.{u^{n - 1}}.u',n \in \mathbb{N}^*.$
$\left( {\sqrt u } \right)' = \frac{{u'}}{{2\sqrt u }}.$

Bảng công thức đạo hàm

Hàm số	Hàm hợp tương ứng
${\left( C \right)^\prime } = 0\,\,\,\,\,;\,\,\,\,{\left( x \right)^\prime } = 1$
${\left( {{x^n}} \right)^\prime } = n.{x^{n - 1}}\,\,\left( {n \in \mathbb{N}\,\,,\,\,n \ge 2} \right)$	${\left( {{u^n}} \right)^\prime } = n.{u^{n - 1}}.u'\,\,\,\,\,,\,\,\,\left( {n \in \mathbb{N}\,\,,\,\,n \ge 2} \right)$
${\left( {\sqrt x } \right)^\prime } = \frac{1}{{2\sqrt x }}\,\,\,\,,\,\,\left( {x > 0} \right)$	$\,\,\,{\left( {\sqrt u } \right)^\prime } = \frac{{u'\,}}{{2\sqrt u }}\,\,\,\,\,,\,\,\left( {u > 0} \right)$
${\left( {\sin x} \right)^\prime } = \cos x\,\,\,$	${\left( {\sin u} \right)^\prime } = u.'\cos u$
${\left( {\cos x} \right)^\prime } = - \sin x\,$	${\left( {\cos u} \right)^\prime } = - u'.\sin u$
${\left( {\tan x} \right)^\prime } = \frac{1}{{{{\cos }^2}x}}\,\,$	$\,\,{\left( {\tan u} \right)^\prime } = \frac{{u'}}{{{{\cos }^2}u}}\,$
${\left( {\cot x} \right)^\prime } = - \frac{1}{{{{\sin }^2}x}}\,\,$	$\,\,{\left( {\cot u} \right)^\prime } = - \frac{{u'}}{{{{\sin }^2}u}}\,$

Đạo hàm cấp 2

Định nghĩa đạo hàm cấp hai

Đạo hàm cấp hai

Hàm số $y=f(x)$ có đạo hàm tại $x \in (a;b).$

Khi đó $y'=f'(x)$ xác định một hàm sô trên (a;b).

Nếu hàm số $y'=f'(x)$ có đạo hàm tại x thì ta gọi đạo hàm của y’ là đạo hàm cấp hai của hàm số $y=f(x)$ tại x.

Kí hiệu: $y''$ hoặc $f''(x).$

Công thức đạo hàm cấp cao (n)

Cho hàm số $y=f(x)$ có đạo hàm cấp $n-1,$ kí hiệu $f^{\left ( n-1 \right )}(x)(n \in \mathbb{N}, n\geq 4)$ và nếu $f^{\left ( n-1 \right )}(x)$ có đạo hàm thì đạo hàm của nó được gọi là đạo hàm câp n của $y=f(x),$ kí hiệu $y^{(n)}$ hoặc $f^{(n)}(x).$