Công thức Hê Rông (Heron): Công thức Hê Rông là gì, chứng minh công thức Hê Rông cho tam giác và các ví dụ…

Công thức Hê Rông là gì?

Công thức này mang tên nhà toán học Heron của Alexandria. Trong hình học, công thức Heron là công thức tính diện tích của một tam giác theo độ dài 3 cạnh.

Công thức Hê Rông

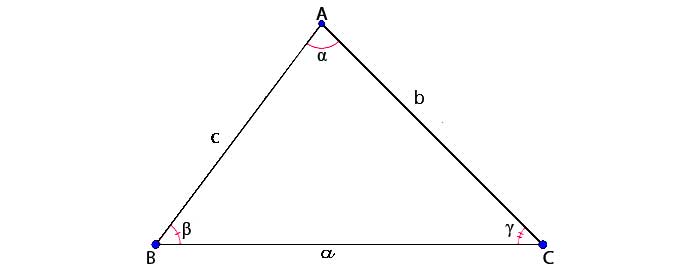
Gọi S là diện tích và độ dài 3 cạnh tam giác lần lượt là a, b và c, công thức He Rông được viết như sau:

$S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)}$

Với p là nửa chu vi của tam giác.

$p = \frac{{a + b + c}}{2}$

Công thức Heron còn có thể được viết lại bằng:

$S = \frac{{\sqrt {\left( {a + b + c} \right)\left( {a + b - c} \right)\left( {b + c - a} \right)\left( {c + a - b} \right)} }}{4}$

$S = \frac{{\sqrt {2\left( {{a^2}{b^2} + {a^2}{c^2} + {b^2}{c^2}} \right) - \left( {{a^4} + {b^4} + {c^4}} \right)} }}{4}$

$S = \frac{{\sqrt {{{\left( {{a^2} + {b^2} + {c^2}} \right)}^2} - 2\left( {{a^4} + {b^4} + {c^4}} \right)} }}{4}$

Chứng minh công thức Hê Rông cho tam giác

Cách chứng minh này sử dụng đại số và lượng giác.

Gọi a, b, c lần lượt là 3 cạnh của tam giác và A, B, C lần lượt là các góc đối diện của các cạnh. Theo hệ quả định lý cosin, ta có:

$\cos \left( C \right) = \frac{{{a^2} + {b^2} - {c^2}}}{{2ab}}$

Từ đó:

$\sin \left( C \right) = \sqrt {1 - {{\cos }^2}\left( C \right)} = \frac{{\sqrt {4{a^2}{b^2} - {{\left( {{a^2} + {b^2} - {c^2}} \right)}^2}} }}{{2ab}}$

Dựa vào đường cao và sin của góc C. Ta có công thức tính diện tích tam giác ABC:

$\begin{array}{l} S = \frac{1}{2}ab\sin (C)\\ = \frac{1}{4}\sqrt {4{a^2}{b^2} - {{({a^2} + {b^2} - {c^2})}^2}} \\ = \frac{1}{4}\sqrt {(2ab - ({a^2} + {b^2} - {c^2}))(2ab + ({a^2} + {b^2} - {c^2}))} \\ = \frac{1}{4}\sqrt {({c^2} - {{(a - b)}^2}({{(a + b)}^2} - {c^2})} \\ = \frac{1}{4}\sqrt {(c - (a - b))((c + (a - b))((a + b) - c))((a + b) + c)} \\ = \sqrt {p(p - a)(p - c)(p - c)} \end{array}$

=> dpcm.

Ví dụ tính diện tích tam giác áp dụng công thức Hê Rông

Câu hỏi:
Tam giác ABC có độ dài các cạnh là 6, 8, 10. Tính diện tích tam giác ABC?
Lời giải:
a. Cách 1:
Ta dễ nhận thấy rằng tam giác này vuông( Theo định lý Pytago), nên cạnh lớn nhất là cạnh huyền =10.

Vậy diện tích bằng $\frac{1}{2}.6.8=24$