Công thức số phức: Phép cộng trừ nhân chia số phức, công thức số phức lượng giác…

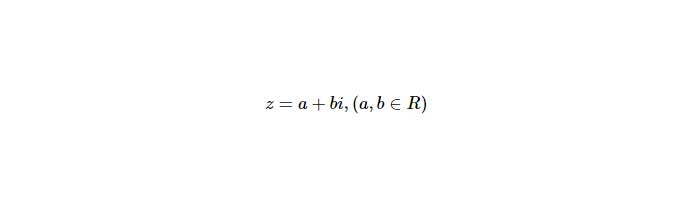
Công thức cộng, trừ và nhân hai số phức

Cho hai số phức ${z_1} = a + bi,\,\,{z_2} = c + di\,(a,b,c,d \in \mathbb{R}),$ ta có:

$z_1+z_2=(a + bi) + ( c + di) = (a + c) + (b + d)i$
$z_1-z_2=(a + bi) - ( c + di) = (a - c) + (b - d)i$
$z_1.z_2=(a + bi)( c + di) = (ac - bd) + (ad + bc)i$

Nhận xét

Phép cộng và phép nhân số phức được thực hiện tương tự như đối với số thực, với chú ý $i^2=-1.$
Với mọi $z,z'\in\mathbb{C}$ :
$z + \overline z = 2a$ (với $z = a + bi$ )
= + ‘
$z.\overline z = {\left| z \right|^2} = {\left| {\overline z } \right|^2}$
$\left| {z.z'} \right| = \left| z \right|.\left| {z'} \right|$
$\left| {z + z'} \right| \le \left| z \right| + \left| {z'} \right|$

Phép chia hai số phức

Cho hai số phức ${z_1} = a + bi,\,\,{z_2} = c + di\,(a,b,c,d \in \mathbb{R}),$ ta có:

$\frac{{c + di}}{{a + bi}} = \frac{{\left( {c + di} \right)(a - bi)}}{{{a^2} + {b^2}}} = \frac{{ac + bd}}{{{a^2} + {b^2}}} + \frac{{ad - bc}}{{{a^2} + {b^2}}}i$

(Nhân cả tử và mẫu với $a - bi$ (số phức liên hợp của mẫu)).

Chú ý
Với số phức $z\ne0$ ta có:

Số phức nghịch đảo của $z$ : ${z^{ - 1}} = \frac{1}{{{{\left| z \right|}^2}}}\overline z .$
Thương của $z'$ chia cho $z$ : $\frac{{z'}}{z} = z'.{z^{ - 1}} = \frac{{z'.\overline z }}{{{{\left| z \right|}^2}}} = \frac{{z'.\overline z }}{{z.\overline z }}.$

Công thức số phức lượng giác

Để viết số phức $z = a + bi,(a,b \in R)$ dưới dạng lượng giác $z = r(c{\rm{os}}\varphi + i\sin \varphi )$ , trước hết ta biến đổi: $z = \sqrt {{a^2} + {b^2}} (\frac{a}{{\sqrt {{a^2} + {b^2}} }} + \frac{b}{{\sqrt {{a^2} + {b^2}} }}i).$
Như vậy: $r = \sqrt {{a^2} + {b^2}}.$ Đặt $c{\rm{os}}\varphi = \frac{a}{{\sqrt {{a^2} + {b^2}} }}$ và $\sin \varphi = \frac{b}{{\sqrt {{a^2} + {b^2}} }}.$
Từ đó suy ra $\varphi$ là $1$ $acgumen$ của $z.$

Các công thức biến đổi lượng giác cần lưu ý

$1 + c{\rm{os}}\varphi + i\sin \varphi$ $= 2{\cos ^2}\frac{\varphi }{2} + 2i\sin \frac{\varphi }{2}c{\rm{os}}\frac{\varphi }{2}$ $= 2\cos \frac{\varphi }{2}\left[ {c{\rm{os}}\frac{\varphi }{2} + i \sin \frac{\varphi }{2}} \right].$
$1 + i\tan \varphi = 1 + i\frac{{\sin \varphi }}{{c{\rm{os}}\varphi }}$ $= \frac{1}{{c{\rm{os}}\varphi }}(c{\rm{os}}\varphi + i \sin \varphi ).$

Ví dụ áp dụng công thức số phức

Ví dụ 1:
Cho số phức $\frac{{\sqrt 3 }}{2} - \frac{1}{2}i.$ Tìm các số phức sau $\overline z$ ; $z^2$ ; ${\left( {\overline z } \right)^3}$ ; $1+z+z^2.$

Lời giải:
$z = \frac{{\sqrt 3 }}{2} - \frac{1}{2}i \Rightarrow \overline z = \frac{{\sqrt 3 }}{2} + \frac{1}{2}i$
${z^2} = {\left( {\frac{{\sqrt 3 }}{2} - \frac{1}{2}i} \right)^2} = \frac{3}{4} + \frac{1}{4}{i^2} - \frac{{\sqrt 3 }}{2}i = \frac{1}{2} - \frac{{\sqrt 3 }}{2}i$
$\Rightarrow {\left( {\overline z } \right)^2} = {\left( {\frac{{\sqrt 3 }}{2} + \frac{1}{2}i} \right)^2} \\= \frac{3}{4} + \frac{1}{4}{i^2} + \frac{{\sqrt 3 }}{2}i = \frac{1}{2} + \frac{{\sqrt 3 }}{2}i$

${\left( {\overline z } \right)^3} = {\left( {\overline z } \right)^2}.\overline z = \left( {\frac{1}{2} + \frac{{\sqrt 3 }}{2}i} \right)\left( {\frac{{\sqrt 3 }}{2} + \frac{1}{2}i} \right) \\= \frac{{\sqrt 3 }}{4} + \frac{1}{2}i + \frac{3}{4}i - \frac{{\sqrt 3 }}{4} = i$
$1 + z + {z^2} = 1 + \frac{{\sqrt 3 }}{2} - \frac{1}{2}i + \frac{1}{2} - \frac{{\sqrt 3 }}{2}i \\= \frac{{3 + \sqrt 3 }}{2} - \frac{{1 + \sqrt 3 }}{2}i$

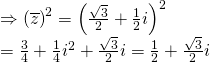
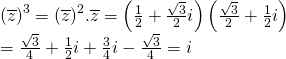
Ví dụ 2:
Tìm phần thực, phần ảo và tính mô đun của số phức $z$ biết: $\overline z = {\left( {\sqrt 2 + i} \right)^2}\left( {1 - i\sqrt 2 } \right).$

Lời giải:
Ta có:

$\begin{array}{l} \overline z = {\left( {\sqrt 2 + i} \right)^2}\left( {1 - i\sqrt 2 } \right) \\= \left( {2 + {i^2} + 2i\sqrt 2 } \right)\left( {1 - i\sqrt 2 } \right) = 5 + i\sqrt 2 \\ \Rightarrow z = 5 - i\sqrt 2 \end{array}$

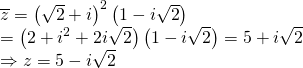
Vậy z có phần thực bằng 5; phần ảo bằng $-\sqrt2$ .

Môđun: $\left| z \right| = \sqrt {{5^2} + {{\left( { - \sqrt 2 } \right)}^2}} = 3\sqrt 3 .$

Ví dụ 3:
Tìm số phức $z$ biết $(2z - i)(1 + i) + (\overline z + 1)(1 - i) = 2 - 2i.$

Lời giải:
Cho $z=a+bi (a,b\in\mathbb{R})$ suy ra $\overline z = a - bi,$ từ giải thiết bài toán ta có:

$(2a + 2bi - 1)(1 + i) + (a - bi + 1)(1 - i) = 2 - 2i$

$\Leftrightarrow 3a - 3b + (a + b - 2)i = 2 - 2i$

$\Leftrightarrow \left\{ \begin{array}{l} 3a - 3b = 2\\ a + b - 2 = - 2 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} a = \frac{1}{3}\\ b = \frac{{ - 1}}{3} \end{array} \right.$

Vậy $z=\frac{1}{3}-\frac{1}{3}i.$

Ví dụ 4:
Tìm tập hợp các điểm biểu diễn số phức z thỏa $\left| {z - 1 + i} \right|=2.$

Lời giải:
Đặt $z=x+yi (x,y\in\mathbb{R})$ ta có: $z - 1 + i = (x - 1) + (y + 1)i$

$\left| {z - 1 + i} \right|=2$ suy ra: $\sqrt {{{(x - 1)}^2} + {{(y + 1)}^2}} = 2 \Leftrightarrow {(x - 1)^2} + {(y + 1)^2} = 4$

Vậy tập hợp các điểm biểu diễn số phức z là đường tròn tâm I(1;-1), bán kính R=2.

Ví dụ 5:
Tìm số phức liên hợp của số phức: $z = (1 + i)(3 - 2i) + \frac{1}{{3 + i}}$ .

Lời giải:
Ta có: $z = 5 + i + \frac{{3 - i}}{{(3 + i)(3 - i)}} = 5 + i + \frac{{3 - i}}{{10}}=\frac{53}{10}+\frac{9}{10}i$

Suy ra số phức liên hợp của số phức z là: $\overline z = \frac{{53}}{{10}} - \frac{9}{{10}}i$ .

Ví dụ 6:
Tìm môđun của số phức $z = \frac{{(1 + i)(2 - i)}}{{1 + 2i}}$ .

Lời giải:
Ta có: $z = \frac{{(1 + i)(2 - i)}}{{1 + 2i}} = \frac{{3 + i}}{{1 + 2i}} = \frac{{\left( {3 + i} \right)\left( {1 - 2i} \right)}}{{\left( {1 + 2i} \right)\left( {1 - 2i} \right)}} = \frac{{5 + i}}{5} = 1 + \frac{1}{5}i.$

Vậy môđun của số phức z là: $\left| z \right| = \sqrt {1 + {{\left( {\frac{1}{5}} \right)}^2}} = \frac{{\sqrt {26} }}{5}$ .

Ví dụ 7:
Tìm phần thực, phần ảo và tính môđun của số phức z thỏa: ${\left( {1 + i} \right)^2}\left( {2 - i} \right)z = 8 + i + \left( {1 + 2i} \right)z.$

Lời giải:
${\left( {1 + i} \right)^2}\left( {2 - i} \right)z = 8 + i + \left( {1 + 2i} \right)z$

$\Leftrightarrow z = \frac{{8 + i}}{{1 + 2i}} = \frac{{\left( {8 + i} \right)\left( {1 - 2i} \right)}}{{\left( {1 + 2i} \right)\left( {1 - 2i} \right)}} = \frac{{10 - 15i}}{5} = 2 - 3i.$

Vậy z có phần thực bằng 2, phần ảo bằng -3, môđun $\left| z \right| = \sqrt {{2^2} + {{\left( { - 3} \right)}^2}} = \sqrt {13} .$

Ví dụ 8:
Tìm số phức z thỏa: $\frac{{(\overline z - 1).(2 - i)}}{{\overline z + 2i}} = \frac{{3 + i}}{2}$

Lời giải:
Điều kiện: $\overline z \ne -2i$ hay $z\ne 2i$

Khi đó: $\frac{{(\overline z - 1).(2 - i)}}{{\overline z + 2i}} = \frac{{3 + i}}{2}$ $\Leftrightarrow 2(\overline z - 1)(2 - i) = (3 + i)(\overline z + 2i)$

$\Leftrightarrow (\overline z - 1)(4 - 2i) = 3\overline z + 6i + iz + 2{i^2}$

$\Leftrightarrow (1 - 3i)\overline z = 2i + 4$

$\Leftrightarrow \overline z = \frac{{2i + 4}}{{1 - 3i}} = \frac{{(2i + 4)(1 + 3i)}}{{10}} = \frac{{ - 1}}{5} + \frac{7}{5}i$

$\Rightarrow z = \frac{{ - 1}}{5} - \frac{7}{5}i$ .

Ví dụ 9:
Tính số phức sau: $z={\left( {\frac{{1 + i}}{{1 - i}}} \right)^{16}} + {\left( {\frac{{1 - i}}{{1 + i}}} \right)^8}.$

Lời giải:
Ta có: $\frac{{1 + i}}{{1 - i}} = \frac{{(1 + i)(1 + i)}}{2} = \frac{{2i}}{2} = i$ $\Rightarrow \frac{{1 - i}}{{1 + i}} = \frac{1}{i} = - i.$

Vậy: ${\left( {\frac{{1 + i}}{{1 - i}}} \right)^{16}} + {\left( {\frac{{1 - i}}{{1 + i}}} \right)^8} = {i^{16}} + {( - i)^8} \\= {({i^2})^8} + {\left( {{{\left( { - i} \right)}^2}} \right)^4} = 1 + 1 = 2.$

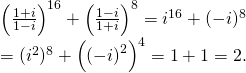
Ví dụ 10: Viết các số phức sau dưới dạng lượng giác:
a. $5$ .
b. $-3$ .
c. $7i$ .
d. $-2i$ .

a. $5 = 5\left( {1 + 0i} \right) = 5\left( {\cos 0 + i\sin 0} \right).$
b. $- 3 = 3\left( { - 1 + 0i} \right) = 3\left( {{\rm{cos}}\pi {\rm{ + sin}}\pi {\rm{i}}} \right).$
c. $7i = 7\left( {0 + i} \right) = 7\left( {\cos \frac{\pi }{2} + i\sin \frac{\pi }{2}} \right).$
d. $- 2i = 2\left( {0 - i} \right)$ $= 2\left( {\cos \left( { - \frac{\pi }{2}} \right) + i\sin \left( { - \frac{\pi }{2}} \right)} \right).$

Ví dụ 11: Viết các số phức sau dưới dạng lượng giác:
a. $1 - i\sqrt 3.$
b. $\sqrt 3 - i\sqrt 3 .$
c. $\frac{1}{3} + \frac{{\sqrt 3 }}{3}i.$
d. $\frac{{7\sqrt 3 }}{3} - 7i.$

a. $1 - i\sqrt 3 = 2\left( {\frac{1}{2} - i\frac{{\sqrt 3 }}{2}} \right)$ $= 2\left[ {\cos \left( { - \frac{\pi }{3}} \right) + i\sin \left( { - \frac{\pi }{3}} \right)} \right].$
b. $\sqrt 3 - i\sqrt 3 = \sqrt 3 \left( {1 - i} \right)$ $= \sqrt 6 \left( {\frac{1}{{\sqrt 2 }} - \frac{i}{{\sqrt 2 }}} \right)$ $= \sqrt 6 \left[ {\cos \left( { - \frac{\pi }{4}} \right) + i\sin \left( { - \frac{\pi }{4}} \right)} \right].$
c. $\frac{1}{3} + \frac{{\sqrt 3 }}{3}i = \frac{2}{3}\left( {\frac{1}{2} + i\frac{{\sqrt 3 }}{2}} \right)$ $= \frac{2}{3}\left( {\cos \frac{\pi }{3} + i\sin \frac{\pi }{3}} \right).$
d. $\frac{{7\sqrt 3 }}{3} - 7i = \frac{{7\sqrt 3 }}{3}\left( {1 - i\sqrt 3 } \right)$ $= \frac{{14\sqrt 3 }}{3}\left( {\frac{1}{2} - i\frac{{\sqrt 3 }}{2}} \right)$ $= \frac{{14\sqrt 3 }}{3}\left[ {\cos \left( { - \frac{\pi }{3}} \right) + i\sin \left( { - \frac{\pi }{3}} \right)} \right].$

Ví dụ 12: Viết các số phức sau dưới dạng lượng giác:
a. $\left( {1 + 3i} \right)\left( {1 + 2i} \right).$
b. $\left( {1 + i} \right)\left[ {1 + \left( {\sqrt 3 - 2} \right)i} \right].$
c. $\left( {\sqrt 2 - 2i} \right).\left[ {\sqrt 2 + \left( {3\sqrt 2 - 4} \right)i} \right].$

a. $\left( {1 + 3i} \right)\left( {1 + 2i} \right)$ $= 1 + 6{i^2} + 3i + 2i$ $= - 5 + 5i = 5\left( { - 1 + i} \right)$
$= 5\sqrt 2 \left( { - \frac{1}{{\sqrt 2 }} + i\frac{1}{{\sqrt 2 }}} \right)$ $= 5\sqrt 2 \left( {\cos \frac{{3\pi }}{4} + i\sin \frac{{3\pi }}{4}} \right).$
b. $\left( {1 + i} \right)\left[ {1 + \left( {\sqrt 3 - 2} \right)i} \right]$ $= 1 - \left( {\sqrt 3 - 2} \right) + \left( {\sqrt 3 - 2 + 1} \right)i$
$= 3 - \sqrt 3 + \left( {\sqrt 3 - 1} \right)i$ $= \sqrt 3 \left( {\sqrt 3 - 1} \right) + \left( {\sqrt 3 - 1} \right)i$
$= \left( {\sqrt 3 - 1} \right)\left( {\sqrt 3 + i} \right)$ $= 2\left( {\sqrt 3 - 1} \right)\left( {\frac{{\sqrt 3 }}{2} + \frac{1}{2}i} \right)$ $= 2\left( {\sqrt 3 - 2} \right)\left( {\cos \frac{\pi }{6} + i\sin \frac{\pi }{6}} \right).$
c. $\left( {\sqrt 2 - 2i} \right).\left[ {\sqrt 2 + \left( {3\sqrt 2 - 4} \right)i} \right]$ $= \left( {2 + 6\sqrt 2 - 8} \right) + \left( {6 - 4\sqrt 2 - 2\sqrt 2 } \right)i$
$= \left( {6\sqrt 2 - 6} \right) + \left( {6 - 6\sqrt 2 } \right)i$ $= \left( {6\sqrt 2 - 6} \right)\left( {1 - i} \right)$
$= \sqrt 2 \left( {6\sqrt 2 - 6} \right)\left( {\frac{1}{{\sqrt 2 }} - \frac{1}{{\sqrt 2 }}i} \right)$ $= \left( {12 - 6\sqrt 2 } \right)\left[ {\cos \left( { - \frac{\pi }{4}} \right) + i\sin \left( { - \frac{\pi }{4}} \right)} \right].$

Ví dụ 13: Viết các số phức sau dưới dạng lượng giác:
a. $\frac{1}{{2 + 2i}}.$
b. $\frac{{3 - i}}{{1 - 2i}}.$
c. $\frac{{1 - i\sqrt 3 }}{{1 + i}}.$

a. Ta có:
$\frac{1}{{2 + 2i}} = \frac{1}{{2\left( {1 + i} \right)}}$ $= \frac{{\sqrt 2 }}{{4\left( {\cos \frac{\pi }{4} + i\sin \frac{\pi }{4}} \right)}}$ $= \frac{{\sqrt 2 }}{4}\left[ {\cos \left( { - \frac{\pi }{4}} \right) + i\sin \left( { - \frac{\pi }{4}} \right)} \right].$
b. $\frac{{3 - i}}{{1 - 2i}} = \frac{{\left( {3 - i} \right)\left( {1 + 2i} \right)}}{{\left( {1 - 2i} \right)\left( {1 + 2i} \right)}}$ $= \frac{{3 + 2 + 6i - i}}{{1 - {{\left( {2i} \right)}^2}}} = \frac{{5 + 5i}}{{1 + 4}}$ $= 1 + i$
$= \sqrt 2 \left( {\frac{1}{{\sqrt 2 }} + \frac{1}{{\sqrt 2 }}i} \right)$ $= \sqrt 2 \left( {\cos \frac{\pi }{4} + i\sin \frac{\pi }{4}} \right).$
c. $\frac{{1 - i\sqrt 3 }}{{1 + i}}$ $= \frac{2}{{\sqrt 2 }}\left[ {\cos \left( { - \frac{\pi }{3} - \frac{\pi }{4}} \right) + i\sin \left( { - \frac{\pi }{3} - \frac{\pi }{4}} \right)} \right]$ $= \sqrt 2 \left[ {\cos \left( {\frac{{ - 7\pi }}{{12}}} \right) + i\sin \left( {\frac{{ - 7\pi }}{{12}}} \right)} \right].$

Ví dụ 14: Viết các số phức sau dưới dạng lượng giác:
a. $1 + \frac{i}{{\sqrt 3 }}.$
b. $1 + \sqrt 3 + \left( {1 - \sqrt 3 } \right)i.$

a. Ta có:
$1 + \frac{i}{{\sqrt 3 }} = 1 + i\tan \frac{\pi }{6}$ $= 1 + i\frac{{\sin \frac{\pi }{6}}}{{\cos \frac{\pi }{6}}}$ $= \frac{1}{{\cos \frac{\pi }{6}}}\left( {\cos \frac{\pi }{6} + i\sin \frac{\pi }{6}} \right)$ $= \frac{2}{{\sqrt 3 }}\left( {\cos \frac{\pi }{6} + i\sin \frac{\pi }{6}} \right).$
b. $1 + \sqrt 3 + \left( {1 - \sqrt 3 } \right)i$ $= 1 + \tan \frac{\pi }{3} + \left( {1 - \tan \frac{\pi }{3}} \right)i$ $= 1 + \frac{{\sin \frac{\pi }{3}}}{{\cos \frac{\pi }{3}}} + \left( {1 - \frac{{\sin \frac{\pi }{3}}}{{\cos \frac{\pi }{3}}}} \right)i$
$= \frac{1}{{\cos \frac{\pi }{3}}}\left( {\cos \frac{\pi }{3} + \sin \frac{\pi }{3}} \right)$ $+ \frac{1}{{\cos \frac{\pi }{3}}}\left( {\cos \frac{\pi }{3} + i\sin \frac{\pi }{3}} \right)i$ $= \frac{1}{{\cos \frac{\pi }{3}}}\left( {\cos \frac{\pi }{3} + \sin \frac{\pi }{3}} \right)$ $- \frac{1}{{\cos \frac{\pi }{3}}}\left( {\sin \frac{\pi }{3} - \cos \frac{\pi }{3}} \right)i$
$= \frac{1}{{\cos \frac{\pi }{3}}}\sqrt 2 \cos \left( {\frac{\pi }{3} - \frac{\pi }{4}} \right)$ $- \frac{1}{{\cos \frac{\pi }{3}}}\sqrt 2 \sin \left( {\frac{\pi }{3} - \frac{\pi }{4}} \right).i$
$= 2\sqrt 2 \left( {\cos \frac{\pi }{{12}} - i\sin \frac{\pi }{{12}}} \right)$ $= 2\sqrt 2 \left[ {\cos \left( { - \frac{\pi }{{12}}} \right) + i\sin \left( { - \frac{\pi }{{12}}} \right)} \right].$
Cách khác:
$1 + \sqrt 3 + \left( {1 - \sqrt 3 } \right)i$ $= \left( {1 + \sqrt 3 } \right)\left( {1 + \frac{{1 - \sqrt 3 }}{{1 + \sqrt 3 }}i} \right)$ $= \left( {1 + \sqrt 3 } \right)\left( {1 + \frac{{\tan \frac{\pi }{4} - \tan \frac{\pi }{3}}}{{1 + \tan \frac{\pi }{4}.\tan \frac{\pi }{3}}}i} \right)$
$= \left( {1 + \sqrt 3 } \right)\left[ {1 + i\tan \left( {\frac{\pi }{4} - \frac{\pi }{3}} \right)} \right]$ $= \left( {1 + \sqrt 3 } \right)\left[ {1 + i\tan \left( { - \frac{\pi }{{12}}} \right)} \right]$
$= \left( {1 + \sqrt 3 } \right)\left[ {1 + i\frac{{\sin \left( { - \frac{\pi }{{12}}} \right)}}{{\cos \left( { - \frac{\pi }{{12}}} \right)}}} \right]$ $= \frac{{1 + \sqrt 3 }}{{\cos \frac{\pi }{{12}}}}\left[ {\cos \left( { - \frac{\pi }{{12}}} \right) + i\sin \left( { - \frac{\pi }{{12}}} \right)} \right].$
Mà $\cos \frac{\pi }{{12}} = \cos \left( {\frac{\pi }{3} - \frac{\pi }{4}} \right)$ $= \cos \frac{\pi }{3}.\cos \frac{\pi }{4} + \sin \frac{\pi }{3}.\sin \frac{\pi }{4}$ $= \frac{1}{{2\sqrt 2 }} + \frac{{\sqrt 3 }}{{2\sqrt 2 }} = \frac{{1 + \sqrt 3 }}{{2\sqrt 2 }}.$
Do đó: $1 + \sqrt 3 + \left( {1 - \sqrt 3 } \right).i$ $= \frac{{1 + \sqrt 3 }}{{\cos \frac{\pi }{{12}}}}\left[ {\cos \left( { - \frac{\pi }{{12}}} \right) + i\sin \left( { - \frac{\pi }{{12}}} \right)} \right]$ $= 2\sqrt 2 \left[ {\cos \left( { - \frac{\pi }{{12}}} \right) + i\sin \left( { - \frac{\pi }{{12}}} \right)} \right].$
Sotayhoctap chúc các bạn học tốt!