Đường trung trực: tính chất đường trung trực, đường trung trực của đoạn thẳng, đường trung trực của tam giác, tính chất đường trung trực của một đoạn thẳng, cách chứng minh đường trung trực…

Đường trung trực là gì?

Trong hình học phẳng, đường trung trực của một đoạn thẳng là đường vuông góc với đoạn thẳng tại trung điểm của đoạn thẳng đó. Trong đường tròn, giao 2 tiếp tuyến thì điểm đó đến tâm là đường trung trực.

Đường trung trực của đoạn thẳng

Đường trung trực của đoạn thẳng là 1 đường thẳng vuông góc với đoạn thẳng và đi qua trung điểm của đoạn thẳng đó.

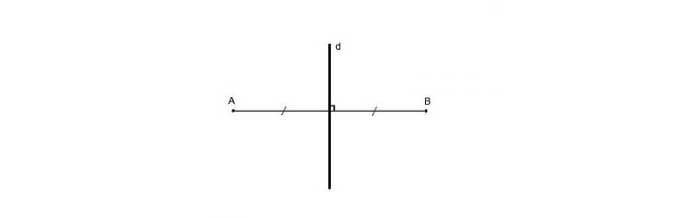
Đường thẳng d được gọi là đường trung trực của đoạn thẳng AB khi và chỉ khi d đi qua trung điểm của đoạn thẳng AB và vuông góc với đoạn thẳng đó.

Tính chất đường trung trực của một đoạn thẳng

Định lý thuận: Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó

Nếu điểm M nằm trên đường trung trực của đoạn thẳng AB thì MA = MB

Định lý đảo: Điểm cách đều hai mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.

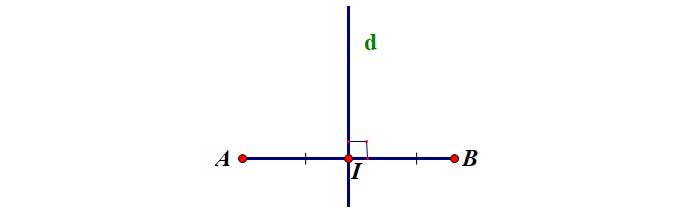
Ta có điểm I cách đều 2 đâu mút của đoạn thẳng AB (IA = IB) nên I nằm trên đường trung trực d của đoạn thẳng AB.

Chứng minh đường trung trực

Xét trường hợp I thuộc AB. Vì IA = IB nên I là trung điểm của đoạn thẳng AB. Suy ra I nằm trên đường trung trực của đoạn AB.
Xét trường hợp I không thuộc AB. Kẻ đoạn thẳng nối I với trung điểm M của đoạn thẳng AB.
Ta có:

$\Delta AMI=\Delta BMI$ (c.c.c).

Suy ra $\widehat{M_{1}}=\widehat{M_{2}}$

Mặt khác: $\widehat{M_{1}}+\widehat{M_{2}}=180^{0}$

Suy ra: $\widehat{M_{1}}=\widehat{M_{2}}=90^{0}$

=> $IM\perp AB$

=> IM là đường trung trực của AB

=> I nằm trên đường trung trực AB

* Nhận xét: Từ định lý thuận và định lý đảo ta có

Tập hợp các điểm cách đều hai mút của một đoạn thẳng là đường trung trực của đoạn thẳng đó.

Đường trung trực của tam giác

Trong tam giác, ba đường trung trực đồng quy tại một điểm, điểm đó cách đều 3 đỉnh của tam giác và là tâm đường tròn ngoại tiếp tam giác. Trong tam giác vuông tâm đường tròn ngoại tiếp là trung điểm của cạnh huyền.

Định lý về đường trung trực của tam giác

Ba đường trung trực của tam giác cùng đi qua một điểm. Giao điểm của ba đường trung trực trong tam giác cách đều ba đỉnh của tam giác và là tâm đường tròn ngoại tiếp tam giác đó.

Tính chất ba đường trung trực của tam giác

Trong tam giác thường

Ba đường trung trực đồng quy tại một điểm, điểm đó cách đều 3 đỉnh của tam giác và là tâm đường tròn ngoại tiếp của tam giác đó.

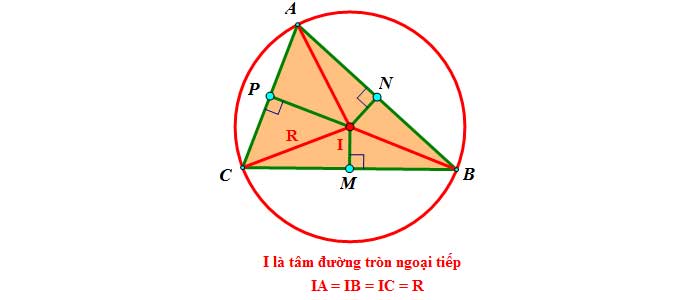
Chứng minh

Vì O nằm trên đường trung trực của đoạn thẳng AC nên ta có OA = OC (1)

O nằm trên đường trung trực của đoạn thẳng AB nên OA= OB = (2)

Từ (1) và (2) suy ra OA = OB = OC

=> O nằm trên đường trung trực của đoạn BC (tính chất đường trung trực của 1 đoạn thẳng)

=> Ba đường trung trực của tam giác ABC cùng đi qua điểm.

Mà OA = OB = OC suy ra O là tâm đường tròn ngoại tiếp tam giác ABC.

Trong tam giác vuông

Tâm đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền tam giác vuông đó. Như vậy, ba đường trung trực trong tam giác vuông cắt nhau tại trung điểm của cạnh huyền tam giác vuông đó.

Trong tam giác cân

Đường trung trực của cạnh đáy đồng thời là đường trung tuyến tương ứng với cạnh này.

Cách viết phương trình đường trung trực của đoạn thẳng

Bước 1:
Tìm vectơ pháp tuyến của đường trung trực và 1 điểm mà nó đi qua.
Bước 2:
Dựa vào tính chất 1: Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó. Tức là nếu điểm M thuộc đường trung trực d của AB thì MA=MB.

Bài tập mẫu về đường trung trực

Ví dụ 1: Cho tam giác ABC. Tìm một điểm O cách đều ba điểm A, B, C.

Giải:

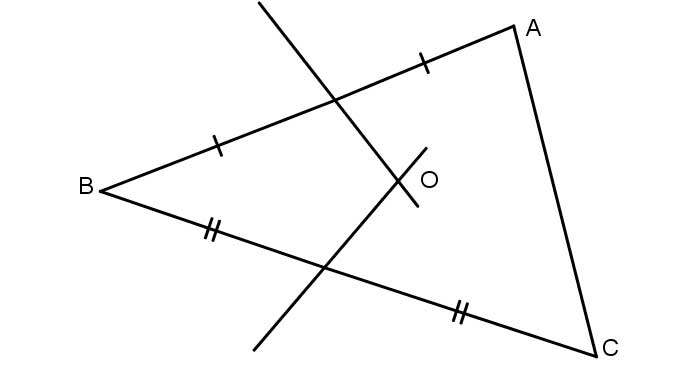
Điểm O cách đều hai điểm A, B nên suy ra điểm O nằm trên đường phân trung trực của đoạn thẳng AB.

Điểm O cách đều hai điểm B, C nên O nằm trên đường trung trực của đoạn thẳng BC.

Điểm O cách đều ba điểm A, B, C nên suy ra O là giao điểm của các đường trung trực của tam giác ABC.

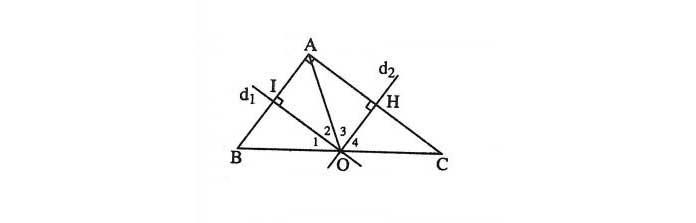
Ví dụ 2: Tam giác ABC có $\widehat A$ là góc tù. Các đường trung trực của AB và của AC cắt nhau ở O và cắt BC theo thứ tự ở P và E. Đường tròn tâm O bán kính OA đi qua những điểm nào trong hình vẽ.

Giải:

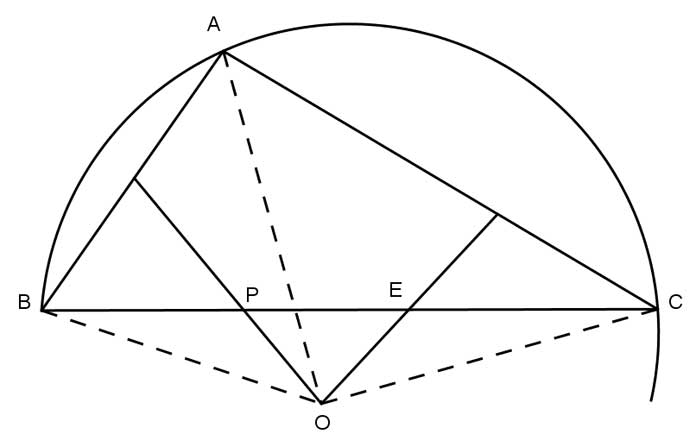
Ta có O thuộc đường trung trực của đoạn AB nên suy ra $OA{\rm{ }} = {\rm{ }}OB\,{\,^{(1)}}$

Lại có O thuộc đường trung trực của đoạn AB nên suy ra $OA{\rm{ }} = {\rm{ }}OC{\,^{\,(2)}}$

Từ (1) và (2) suy ra OA = OB = OC.

Vậy đường tròn (O, OA) đi qua các điểm A, B, C.

Ví dụ 3: Xác định dạng của tam giác có giao điểm các phân giác trùng với giao điểm các đường trung trực.

Giải:

Gọi O là giao điểm các phân giác của $\Delta ABC$ thì ta có $\widehat {OAB} = \widehat {OAC};\widehat {OBA} = \widehat {OBC};\widehat {OCA} = \widehat {OCB}.$ Nhưng O cũng là giao điểm của các đường trung trực nên OA = OB = OC.

Do đó $\widehat {OAB} = \widehat {OBA};\widehat {OAC} = \widehat {OCA}.$ Từ đó suy ra $\widehat A = \widehat B = \widehat C$

Nên $\Delta ABC$ đều.

Ví dụ 4: Cho tam giác ABC và đường phân giác AK của góc A. Biết rằng giao điểm của đường phân giác của tam giác ABK trùng với giao điểm ba đường trung trực của tam giác ABC. Tìm số đo các góc của tam giác ABC.

Giải:

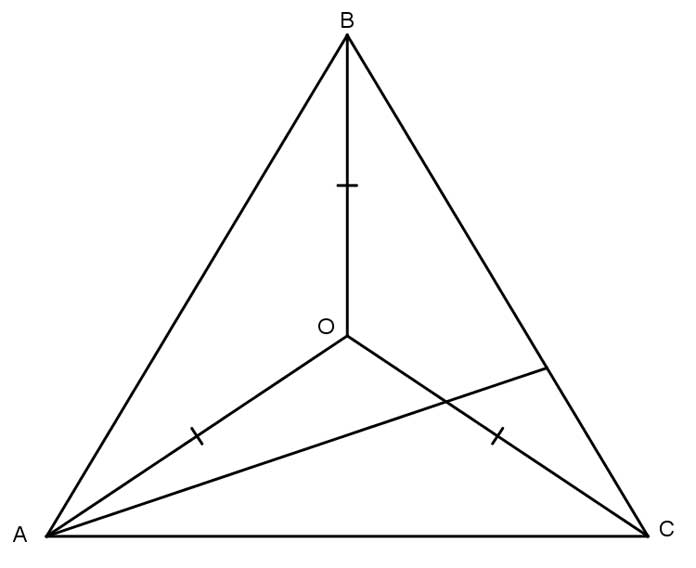
Gọi O là giao điểm của ba đường phân giác của $\Delta ABK$ . Theo đề bài, O là giao điểm của ba đường trung trực của $\Delta ABC$

Vậy OA = OB = OC và các tam giác AOB, BOC, COA đều là các tam giác cân đỉnh O.

Gọi $\widehat {OAB} = a$ thì $\widehat {ABC} = 2a$ và $\widehat {KAB} = 2a.$ Vì AK là đường phân giác của góc BAC nên nếu $\widehat {KAB} = 2a$ thì $\widehat {BAC} = 4a$ .

Ta có: $\Delta AOB = \Delta COB$ nên suy ra AB = CB

Vậy $\Delta ABC$ là tam giác cân đỉnh B.

Suy ra $\widehat {BAC} = \widehat {BAC}.$ Ta đã biết tổng ba góc của một tam giác bằng ${180^0}$ , từ đó:

$2a + 4a + 4a = {180^0} \\\Rightarrow 10a = {180^0} \Rightarrow a = {18^0}$

Vậy số đo các góc của $\Delta ABC$ là:

$\widehat A = {72^0};\,\widehat B = {36^0};\widehat C = {72^0}$

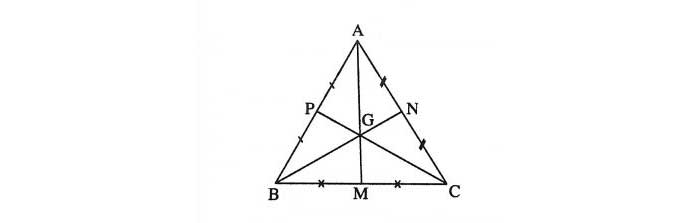
Ví dụ 5: Trên ba cạnh AB, BC và CA của tam giác đều ABC. Lấy các điểm theo thứ tự M, N, P sao cho AM=BN=CP. Gọi O là giao điểm ba đường trung trực của tam giác ABC. Chứng minh O cũng là giao điểm ba đường trung trực của tam giác MNP.

Giải:

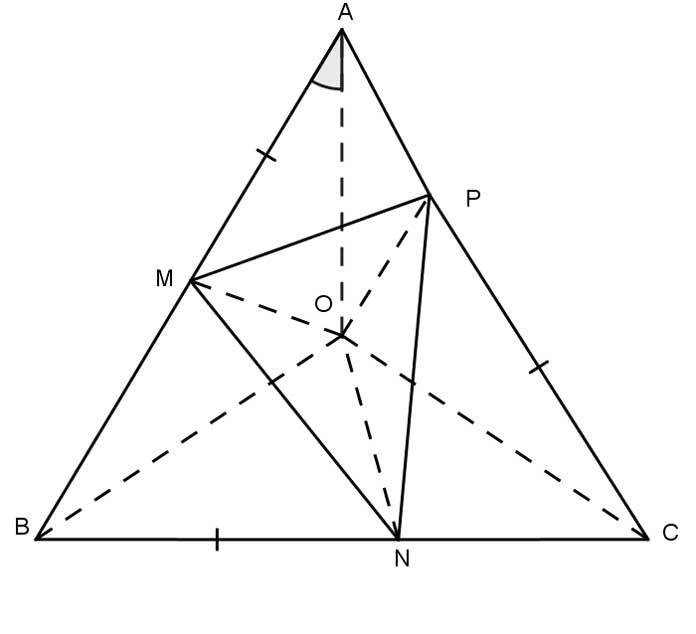
Theo giả thiết O là giao điểm ba đường trung trực của tam giác ABC nên ta có:

OA = OB = OC

$\Rightarrow$ Các tam giác AOM, BON và COP có:

AM = BN = CP (giả thiết)

$\widehat {{A_1}} = \widehat {{B_1}} = \widehat {{C_1}} = {30^0}$ (Vì ABC là tam giác đều nên đường trung trực cũng là đường phân giác) và OA = OB = OC

$\begin{array}{l} \Rightarrow \Delta AOM = \Delta BON = \Delta COP\,\,\,(c.g.c)\\ \Rightarrow \,\,OM = ON = OP\end{array}$

Điều này chứng tỏ O là giao điểm của ba đường trung trực của tam giác MNP.

Trên đây là bài viết về đường trung trực. Sotayhoctap chúc các bạn học tốt!

5/5 - (1 bình chọn)

SỔ TAY HỌC TẬP | SOTAYHOCTAP.COM

Đường trung trực của đoạn thẳng, tam giác và các tính chất

Đường trung trực là gì?

Đường trung trực của đoạn thẳng