Bài viết góc giữa 2 mặt phẳng bao gồm: cách xác định góc giữa 2 mặt phẳng, tính góc giữa 2 mặt phẳng, công thức tính góc giữa 2 mặt phẳng, góc giữa 2 mặt phẳng trong không gian oxyz…
Định nghĩa góc giữa 2 mặt phẳng
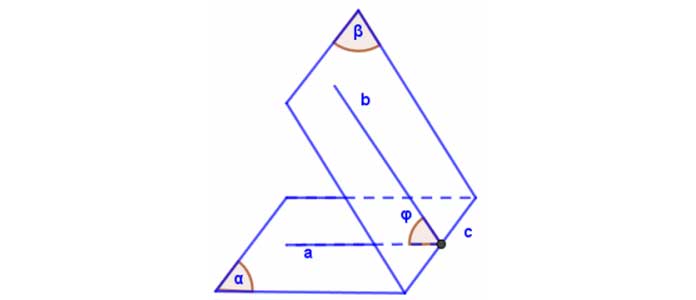
Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó.
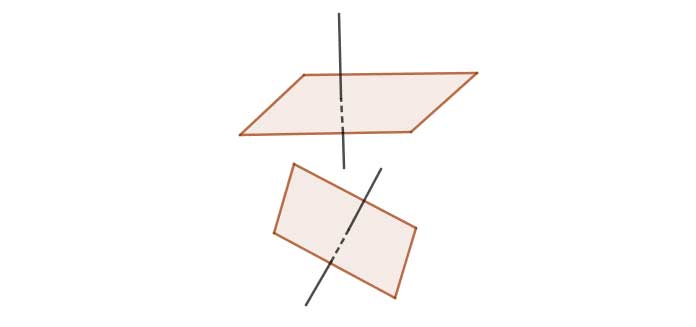
Cách xác định góc giữa 2 mặt phẳng
TH1: Hai mặt phẳng ![]() song song hoặc trùng nhau thì góc giữa chúng bằng
song song hoặc trùng nhau thì góc giữa chúng bằng ![]() .
.
TH2: Hai mặt phẳng ![]() không song song hoặc trùng nhau.
không song song hoặc trùng nhau.
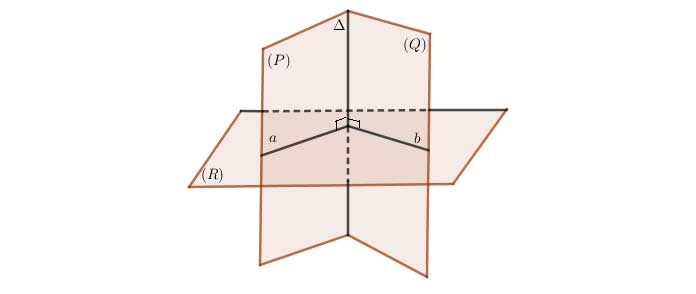
Cách 1:
+) Dựng hai đường thẳng ![]() lần lượt vuông góc với hai mặt phẳng
lần lượt vuông góc với hai mặt phẳng ![]() và
và ![]() .
.
+) Khi đó, góc giữa hai mặt phẳng ![]() và
và ![]() là góc giữa hai đường thẳng
là góc giữa hai đường thẳng ![]() .
.
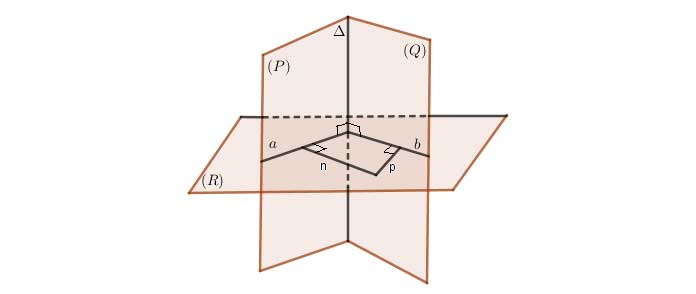
Cách 2:
+) Xác định giao tuyến ![]() của hai mặt phẳng
của hai mặt phẳng ![]() .
.
+) Tìm một mặt phẳng ![]() vuông góc
vuông góc ![]() và cắt và hai mặt phẳng theo các giao tuyến
và cắt và hai mặt phẳng theo các giao tuyến ![]() .
.
+) Góc giữa hai mặt phẳng ![]() là góc giữa
là góc giữa ![]() và
và ![]() .
.
Phương pháp tính góc giữa 2 mặt phẳng
Bài toán: Cho hai mặt phẳng ![]() và
và ![]() cắt nhau, tính góc giữa hai mặt phẳng
cắt nhau, tính góc giữa hai mặt phẳng ![]() và
và ![]()
Ta áp dụng một trong các phương pháp sau đây:
Phương pháp 1
Dựng hai đường thẳng ![]() ,
, ![]() lần lượt vuông góc với hai mặt phẳng
lần lượt vuông góc với hai mặt phẳng ![]() và
và ![]() . Khi đó, góc giữa hai mặt phẳng
. Khi đó, góc giữa hai mặt phẳng ![]() và
và ![]() là
là ![]() Tính góc
Tính góc ![]()
Phương pháp 2
+ Xác định giao tuyến ![]() của hai mặt phẳng
của hai mặt phẳng ![]() và
và ![]()
+ Dựng hai đường thẳng ![]() ,
, ![]() lần lượt nằm trong hai mặt phẳng và cùng vuông góc với giao tuyến
lần lượt nằm trong hai mặt phẳng và cùng vuông góc với giao tuyến ![]() tại một điểm trên
tại một điểm trên ![]() Khi đó:
Khi đó: ![]()
Hiểu cách khác: Ta xác định mặt phẳng phụ ![]() vuông góc với giao tuyến
vuông góc với giao tuyến ![]() mà
mà ![]() ,
, ![]() Suy ra
Suy ra ![]()
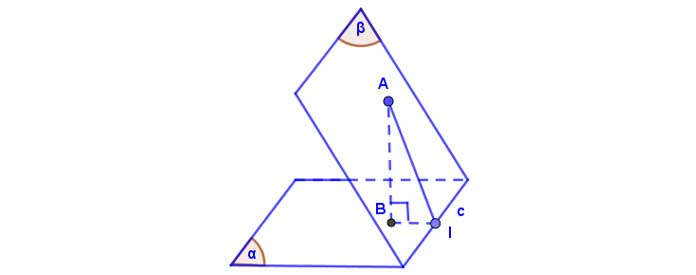
Phương pháp 3 (trường hợp đặc biệt)
Nếu có một đoạn thẳng nối hai điểm ![]() ,
, ![]()
![]() mà
mà ![]() thì qua
thì qua ![]() hoặc
hoặc ![]() ta dựng đường thẳng vuông góc với giao tuyến
ta dựng đường thẳng vuông góc với giao tuyến ![]() của hai mặt phẳng tại
của hai mặt phẳng tại ![]() Khi đó
Khi đó ![]()
Bài tập ví dụ tính góc giữa 2 mặt phẳng
Ví dụ 1. Cho hình chóp tứ giác đều ![]() cạnh đáy
cạnh đáy ![]() bằng
bằng ![]() và
và ![]() Tính
Tính ![]() góc giữa hai mặt phẳng
góc giữa hai mặt phẳng ![]() và
và ![]()
Lời giải:
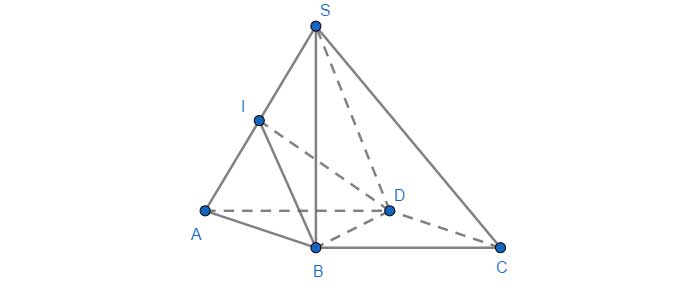
Gọi ![]() là trung điểm
là trung điểm ![]() Do tam giác
Do tam giác ![]() và
và ![]() đều nên:
đều nên:
![]()
![]()
Áp dụng định lý ![]() cho tam giác
cho tam giác ![]() ta có:
ta có:
![]()
![]()
![]()
Vậy ![]()
Ví dụ 2. Cho hình chóp ![]() có đáy
có đáy ![]() là nửa lục giác đều nội tiếp đường tròn đường kính
là nửa lục giác đều nội tiếp đường tròn đường kính ![]() ,
, ![]() vuông góc với
vuông góc với ![]() và
và ![]() Tính góc giữa hai mặt phẳng
Tính góc giữa hai mặt phẳng ![]() và
và ![]()
Lời giải:
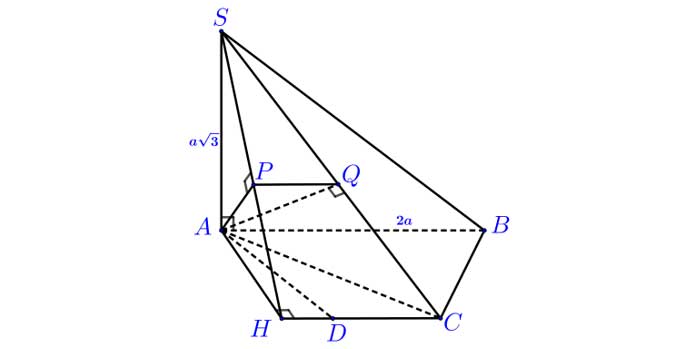
Vì ![]() là nửa lục giác đều nên
là nửa lục giác đều nên ![]()
Dựng đường thẳng đi qua ![]() và vuông góc với
và vuông góc với ![]()
Trong mặt phẳng ![]() dựng
dựng ![]() tại
tại ![]()
![]()
Trong mặt phẳng ![]() dựng
dựng ![]()
![]()
![]()
Dựng đường thẳng đi qua ![]() và vuông góc với
và vuông góc với ![]()
Trong mặt phẳng ![]() dựng
dựng ![]()
Lại có ![]() vì
vì ![]()
![]()
![]()
Vậy ![]()
Suy ra góc giữa hai mặt phẳng ![]() và
và ![]() là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng ấy là
là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng ấy là ![]() và
và ![]()
Ta tính góc ![]() , có
, có ![]()
![]()
![]()
![]()
Tam giác ![]() vuông cân tại
vuông cân tại ![]()
![]()
![]() vuông tại
vuông tại ![]()
![]()
![]()
![]()
Ví dụ 3. Cho hình chóp ![]() có đáy
có đáy ![]() là tam giác vuông cân với
là tam giác vuông cân với ![]() ,
, ![]() ,
, ![]() Gọi
Gọi ![]() lần lượt là trung điểm của các cạnh
lần lượt là trung điểm của các cạnh ![]() Tính
Tính ![]() góc giữa hai mặt phẳng
góc giữa hai mặt phẳng ![]() và
và ![]()
Lời giải:
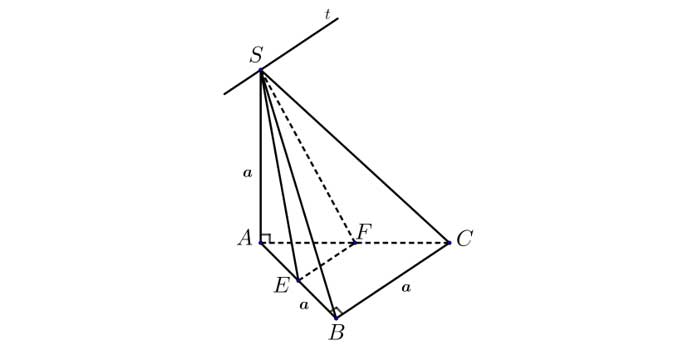
Nhận xét: Giao tuyến của hai mặt phẳng ![]() và
và ![]() là đường thẳng
là đường thẳng ![]() đi qua
đi qua ![]() và song song với
và song song với ![]() và
và ![]() nên ta xác định hai đường thẳng qua
nên ta xác định hai đường thẳng qua ![]() và lần lượt nằm trong hai mặt phẳng
và lần lượt nằm trong hai mặt phẳng ![]() và
và ![]() và cùng vuông góc với
và cùng vuông góc với ![]() (ta đi chứng minh hai đường thẳng đó là
(ta đi chứng minh hai đường thẳng đó là ![]() và
và ![]() ).
).
Vì 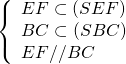
![]() giao tuyến của
giao tuyến của ![]() và
và ![]() là đường thẳng qua
là đường thẳng qua ![]() , song song với
, song song với ![]() , là
, là ![]()
Ta có ![]()
![]()
![]() hay
hay ![]()
Tương tự ![]()
![]() mà
mà ![]()
![]()
Vậy ![]() và
và ![]() cùng đi qua
cùng đi qua ![]() và cùng vuông góc với
và cùng vuông góc với ![]() nên góc giữa hai mặt phẳng
nên góc giữa hai mặt phẳng ![]() và
và ![]() bằng góc giữa hai đường thẳng
bằng góc giữa hai đường thẳng ![]() và
và ![]()
Ta tính góc ![]()
Có ![]() ;
; ![]() ;
; ![]()
Theo định lí ![]() ta có:
ta có: ![]()
![]()
![]()
Sotayhoctap chúc các bạn học tốt!




