Mục lục bài viết

Định nghĩa đường parabol
Phương trình Parabol
Phương trình chính tắc của parabol
Xác định tọa độ đỉnh của parabol
Ví dụ parabol

Parabol: định nghĩa đường Parabol, phương trình Parabol, phương trình chính tắc của parabol, xác định tọa độ đỉnh của parabol…

Định nghĩa đường parabol

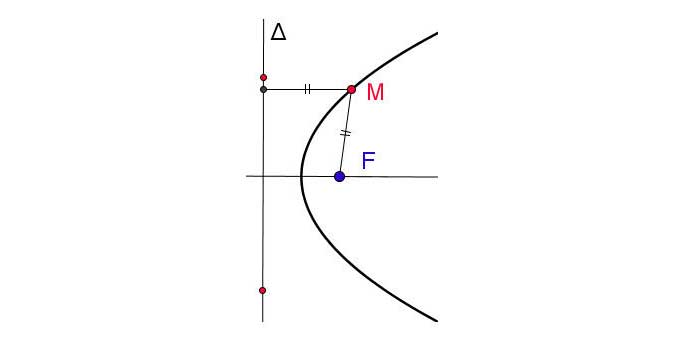
Cho một điểm F cố định và một đường thẳng cố định không đi qua F. Tập hợp các điểm M cách đều F và được gọi là đường parabol (hay parabol) (h. 92).

Điểm F được gọi là tiêu điểm của parabol.

Đường thẳng được gọi là đường chuẩn của parabol.

Khoảng cách từ F đến được gọi là tham số tiêu của parabol.

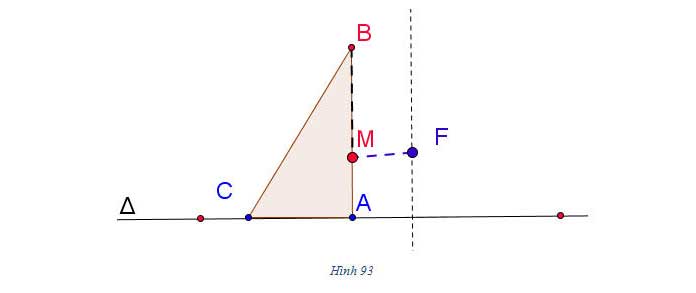
Ta có thể vẽ parabol với tiêu điểm F và đường chuẩn như sau (h. 93) : Lấy một êke ABC (vuông ở A) và một đoạn dây không đàn hồi, có độ dài bằng AB. Đính một đầu dây vào điểm F, đầu kia vào đỉnh B của êke. Đặt êke sao cho cạnh AC nằm trên , lấy đầu bút chì ép sát sợi dây rồi cho cạnh AC của êke trượt trên . Khi đó đầu M của bút chì sẽ vạch nên một phần của parabol (vì ta luôn có MF = MA).

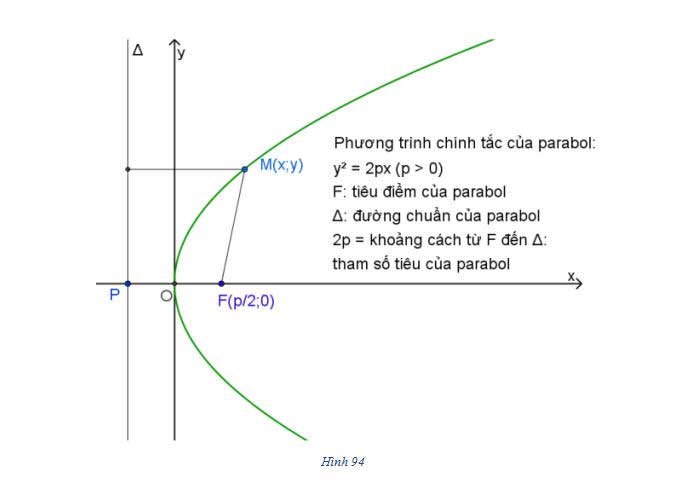
Phương trình Parabol

Phương trình Parabol được biểu diễn như sau: $y = a^{2}+bx+c$

Hoành độ của đỉnh là $\frac{-b}{2a}$

Thay tọa độ trục hoành vào phương trình, ta tìm được hoành độ Parabol có công thức dưới dạng: $\frac{b^{2}-4ac}{4a}$

Phương trình chính tắc của parabol

Phương trình chính tắc của parabol được biểu diễn dưới dạng:

$y^{2}= 2px (p> 0)$

Chứng minh:

Cho parabol với tiêu điểm F và đường chuẩn $\Delta$ .

Kẻ $FP\perp \Delta (P \in \Delta )$ . Đặt FP = p.

Ta chọn hệ trục tọa độ Oxy sao cho O là trung điểm của FP và điểm F nằm trên tia Ox.

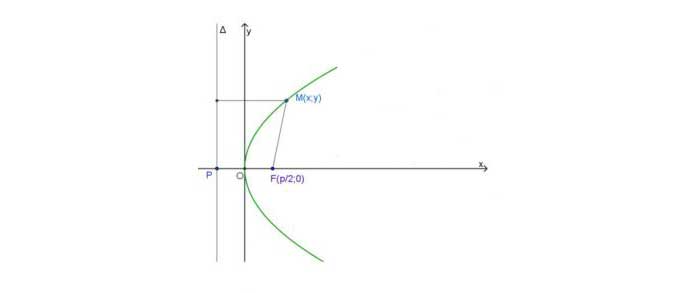
Suy ra ta có $F= (\frac{P}{2};0), P= (-\frac{P}{2};0)$

Và phương trình của đường thẳng $\Delta$ là $x + \frac{p}{2} = 0$

Điểm M(x ; y) nằm trên parabol đã cho khi và chỉ khi khoảng cách MF bằng khoảng cách từ M tới $\Delta$ , tức là:

$\sqrt{(x- \frac{p}{2})^{2}+ y^{2}} = \left | x + \frac{p}{2} \right |$

Bình phương 2 vế của đẳng thức rồi rút gọn, ta được phương trình chính tắc của parabol:

$y^{2}= 2px (p> 0)$

Chú ý: Ở môn đại số, chúng ta gọi đồ thị của hàm số bậc hai $y = ax^{2} + bx + c$ là một đường parabol.

Xác định tọa độ đỉnh của parabol

Ví dụ: Xác định tọa độ của đỉnh và các giao điểm với trục tung, trục hoành (nếu có) của mỗi parabol.

a) $y = x^{2} - 3x + 2$

b) $y = -2x^{2} + 4x - 3$

Hướng dẫn:

a) $y = x^{2} - 3x + 2$ . Có hệ số: a = 1, b = – 3, c = 2.

$\Delta = b^{2} - 4ac$ = (-3).2 – 4.1.2 = – 1

Tọa độ đỉnh của đồ thị hàm số $I(\frac{-b}{2c};\frac{-\Delta }{4a})$

Hoành độ đỉnh $x_{I} = \frac{-b}{2a} = \frac{-3}{2}$

Tung độ đỉnh $y_{I} = \frac{-\Delta }{4a} = \frac{-1}{4}$

Vậy đỉnh parabol là $I (\frac{-3}{2};\frac{-1}{4})$

Cho x = 0 → y = 2 ⇒ A(0; 2) là giao điểm của đồ thị hàm số với trục tung.

Cho y = 0 ↔ $x^{2} - 3x + 2 = 0$ ⇔ $\left\{\begin{matrix} x_{1} = 1 & \\ x_{2} = 2 & \end{matrix}\right.$

Suy ra B(1; 0) và C(2; 0) là giao điểm của đồ thị hàm số với trục hoành.

b) Cho $y = -2x^{2} + 4x - 3$ . Có a = -2 , b = 4, c = -3

Δ = $\Delta = b^{2} - 4ac$ = 42 – 4. (-2).(-3) = – 8

Tọa độ đỉnh của đồ thị hàm số $I(\frac{-b}{2c};\frac{-\Delta }{4a})$

Hoành độ đỉnh $x_{I} = \frac{-b}{2a} = 1 Tung độ đỉnh [latex]y_{I} = \frac{-\Delta }{4a}= 1 Vậy đỉnh parabol là I (1; 1) Cho x = 0 => y = - 3 ⇒ A(0; -3) là giao điểm của đồ thị hàm số với trục tung. Cho y = 0 => [latex]-2x^{2} + 4x - 3 = 0$

$\Delta$ = b2 – 4ac = $4^{2}$ – 4. (-2).(-3) = – 8 < 0.

Phương trình vô nghiệm ⇒ không tồn tại giao điểm của hàm số với trục hoành.

Ví dụ parabol

Xác định parabol y = ax² + bx + 2, biết rằng parabol đó:

a) Đi qua hai điểm M(1; 5) và N(- 2; 8);

b) Đi qua hai điểm A(3;- 4) và có trục đối xứng là x=-3/2

c) Có đỉnh là I(2;- 2);

d) Đi qua điểm B(- 1; 6) và tung độ của đỉnh là -1/4

Hướng dẫn.

a) M(1; 5) ∈ (P) nên tọa độ của M thỏa mãn parabol:y_M = ax_M² + bx_M + 2 ↔ 5 = a.1² + b.1 + 2. (1)

N(- 2; 8) ∈ (P) nên tọa độ của N thỏa mãn parabol:y_N = ax_N² + bx_N + 2 ↔ 8 = a.(- 2)² + b.(- 2) + 2 (2)

Giải hệ phương trình:(1) và (2) ta được a = 2, b = 1.

Vậy Parabol có phương trình là: y = 2x² + x + 2.

b) Đi qua điểm A(3;- 4) và có trục đối xứng là x=-3/2

A(3;- 4) ∈ (P) nên tọa độ của A thỏa mãn parabol:y_A = ax_A² + bx_A + 2 ↔ -4 = a.3² + b.3 + 2 (1)
y = ax² + bx + 2 có trục đối x = -b/2a ↔ -3/2 = -b/2a ↔ b = 3a (2)

Giải hệ phương trình (1) và (2) ta có a = -1/3, b = -1

Parabol: y = -1/3x² – x + 2.

c) Cho hàm số y = ax² + bx + 2

Tọa độ đỉnh của hàm số là I(-b/2a; -Δ/4a). Theo đề bài cho tọa độ đỉnh là I(2;- 2)

-b/2a = 2 ↔ -b = 4a (1)
-Δ/4a = – 2 ↔ -(b² – 8a )= -8a (2)

Giải hệ phương trình (1) và (2) ta thu được kết quả là b = 0 và b = -4

với b = 0 → a = 0 → y = 2 là 1 đường thẳng (loại)

với b = -4 → a = 1

Kết luận Parabol cần tìm là Parabol: y = x² – 4x + 2.

d) Đi qua điểm B(- 1; 6) và tung độ của đỉnh là -1/4

B(- 1; 6) ∈ (P) nên tọa độ của B thỏa mãn parabol:y_B = ax_B² + bx_B + 2 ↔ 6 = a.(-1)²+ b.(-1) + 2
Tọa độ đỉnh I(-b/2a; -Δ/4a) tung độ của tọa độ đỉnh là y_I = -Δ/4a = -1/4 ↔ – (b² – 8a )= -a (2)

Giải hệ phương trình (1) và (2) thu được kết quả

a = 16 →b = 12
a = 1 → b = -3

Parabol: y = 16x² + 12x + 2 hoặc y = x² – 3x + 2.
Sotayhoctap chúc các bạn học tốt!

Định nghĩa đường parabol – Phương trình Parabol và các xác định tọa độ đỉnh

Định nghĩa đường parabol

Phương trình Parabol

Phương trình chính tắc của parabol

Xác định tọa độ đỉnh của parabol

Ví dụ parabol

Bài viết cùng chuyên mục

Trả lời Hủy