Tích vô hướng của 2 vectơ: Góc giữa hai vectơ, Định nghĩa tích vô hướng của hai vectơ, Tính chất của tích vô hướng, Biểu thức tọa độ của tích vô hướng…
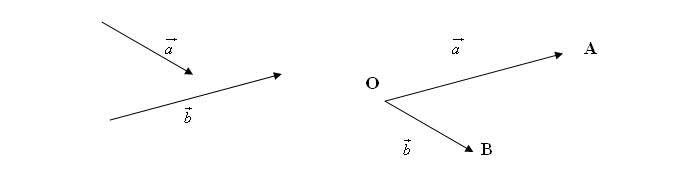
Góc giữa hai vectơ
Cho hai vectơ ![]() và
và ![]() được mô tả như hình sau:
được mô tả như hình sau:
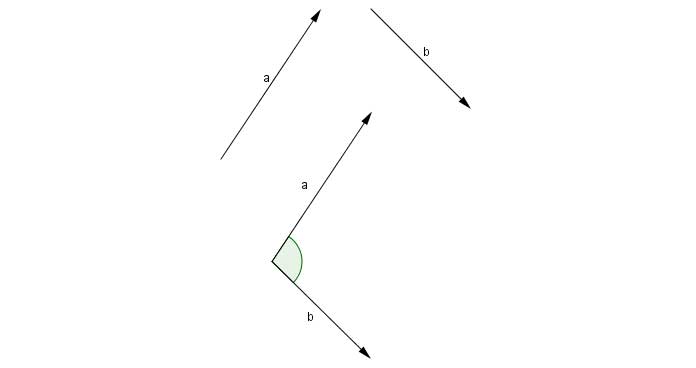
Số đo góc trên được gọi là số đo của góc giữa hai vectơ ![]() và
và ![]() .
.
Nếu số đo ấy bằng 90 độ, ta nói ![]() vuông góc với
vuông góc với ![]() .
.
Định nghĩa tích vô hướng của hai vectơ
Tích vô hướng của hai vectơ ![]() và
và ![]() là một số (đại lượng đại số), được kí hiệu là
là một số (đại lượng đại số), được kí hiệu là ![]() và được xác định bởi công thức
và được xác định bởi công thức
![]()
Bình phương vô hướng:
Với mỗi vectơ ![]() tùy ý, tích vô hướng
tùy ý, tích vô hướng ![]() được kí hiệu là
được kí hiệu là ![]() được gọi là bình phương vô hướng
được gọi là bình phương vô hướng
Ta có: ![]()
Như vậy: Bình phương vô hướng của một vectơ bằng bình phương độ dài của vectơ đó
Tính chất của tích vô hướng
a) Định lí
Với ba vectơ ![]() tùy ý và một số thực k, ta có:
tùy ý và một số thực k, ta có:
![]() (tính chất giao hoán)
(tính chất giao hoán)
![]()
![]()
![]() (tính chất phân phối tổng hiệu)
(tính chất phân phối tổng hiệu)
b) Phương tích của một điểm đối với một đường tròn
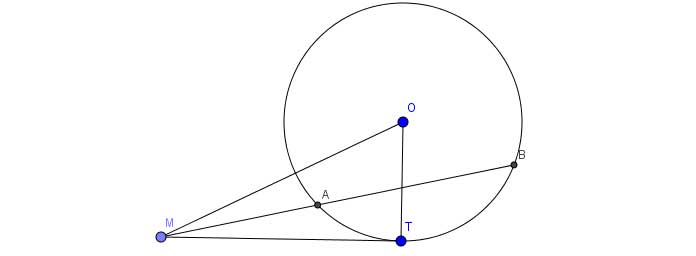
Ta dễ dàng chứng minh được ![]() thông qua việc chứng minh tam giác đồng dạng
thông qua việc chứng minh tam giác đồng dạng
Mặc khác theo định lý Pytago vào tam giác OMT vuông tại T (vì MT là tiếp tuyến)
Ta có: ![]()
Theo ý trên: ![]() (vì M, A, B thẳng hàng)
(vì M, A, B thẳng hàng)
Vậy: ![]()
Đây chính là phương tích của điểm M đối với đường tròn (O).
Biểu thức tọa độ của tích vô hướng
Cho hai vectơ ![]() . Khi đó:
. Khi đó:
![]()
![]()
![]()
![]()
Ví dụ cho tích vô hướng của 2 vectơ
Ví dụ 1:
Tính tích vô hướng của ![]() và
và ![]() biết chúng tạo với nhau một góc
biết chúng tạo với nhau một góc ![]()
Lời giải:
Áp dụng công thức tính tích vô hướng của hai vectơ, ta có: ![]()
![]()
Ví dụ 2:
Cho hình vuông ABCD cạnh a đường chéo BD. Tính các tích vô hướng sau: ![]() ,
, ![]() và
và ![]()
Lời giải:
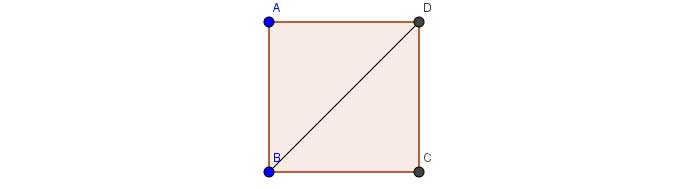
Vì ![]() nên
nên ![]()
![]()
![]()
Ví dụ 3:
Tính giá trị của biểu thức ![]() biết
biết ![]()
Lời giải:
Ta có: ![]()
![]()
![]()
![]()
![]()
Ví dụ 4:
Chứng minh biểu thức sau không phụ thuộc vào x:
![]()
Lời giải:
Ta có:
![]()
![]()
![]()
![]()
![]()
Vậy biểu thức trên không phụ thuộc vào giá trị của góc x
Sotayhoctap chúc các bạn học tốt!




