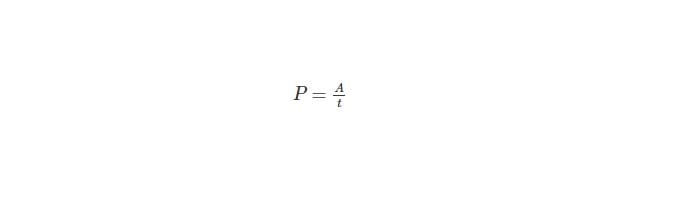Định luật bảo toàn năng lượng: định luật bảo toàn và chuyển hóa năng lượng, công , công suất trung bình , công suất tực thời , động năng , liên hệ giữa động năng và công , thế năng trong trường , liên hệ giữa thế năng trọng trường và công , công của trọng lực , thế năng đàn hồi , liên hệ giữa thế năng đàn hồi và công , cơ năng , định luật bảo toàn cơ năng , độ cao động năng bằng n lần thế năng , hiệu suất…
Định luật bảo toàn năng lượng
Định luật bảo toàn và chuyển hóa năng lượng
Năng lượng không tự nhiên sinh ra cũng không tự nhiên mất đi mà nó chỉ chuyển hóa từ dạng này sang dạng khác hoặc từ vật này sang vật khác. Đây được coi là định luật cơ bản của vật lý học.
Ví dụ:
Nếu thả một hòn bi từ trên cao xuống một cái chén thì năng lượng của hòn bi là thế năng hấp dẫn, rơi vào chén và chuyển động quanh thành chén là động năng, đồng thời phát ra tiếng động là âm năng. Ngoài ra bi còn ma sát với thành chén tạo ra nhiệt năng, vậy ta có thể thấy từ một dạng năng lượng là thế năng đã chuyển hóa thành ba dạng năng lượng như đã nêu ở trên.
Bảo toàn năng lượng trong dao động cơ
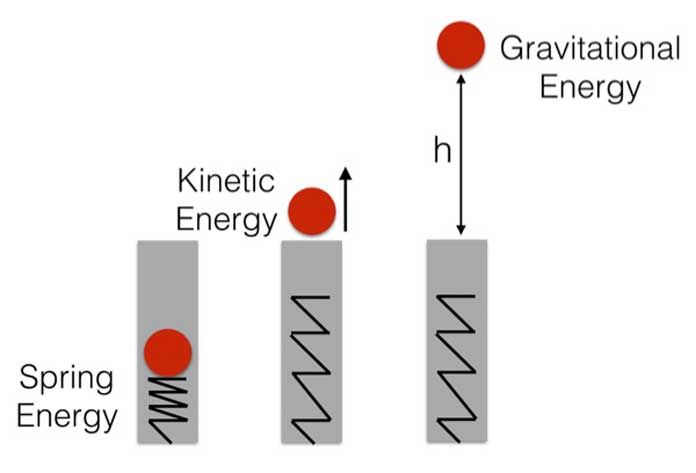
Năng lượng trong dao động cơ được gọi là cơ năng. Cơ năng bằng tổng động năng và thế năng. Trong một hệ kín cơ năng không đổi.
Khái niệm động năng
Động năng của một vật là năng lượng có được từ chuyển động của vật đó. Nó được định nghĩa là công cần thực hiện để gia tốc một vật với khối lượng cho trước từ trạng thái nghỉ tới vận tốc hiện thời của vật .
Động năng của một vật rơi tự do được tính bằng công thức: ![]()
Trong đó:
- Wd: động năng của vật (J)
- m: khối lượng của vật (g)
- v: vận tốc của vật (m/s)
Khái niệm thế năng
Thế năng là một đại lượng vật lý đặc trưng cho khả năng sinh công của vật. Thế năng của một vật rơi tự do được tính bằng công thức: ![]()
Trong đó:
- Wt: Thế năng của vật (J)
- m: Trọng lượng của vật (g)
- h: Độ cao của vật khi rơi tự do (m)
Biểu thức bảo toàn cơ năng
![]()
Trong đó:
- Wd1: Động năng của vật ở vị trí có vận tốc v1
- Wd2: Động năng của vật ở vị trí có vận tốc v2
- Wt1: Thế năng của vật ở độ cao h1
- Wt2: Thế năng của vật ở độ cao h2
Dựa vào biểu thức trên ta có thể thấy rằng:
Một vật khi rơi tự do, tại thời điểm thế năng cực đại thì động năng bằng 0. Động năng cực đại thì thế năng bằng 0. Động năng tăng thì thế năng giảm. Động năng giảm thì thế năng tăng, nhưng tổng động năng và thế năng là một đại lượng không đổi.
Các công thức liên quan định luật bảo toàn năng lượng
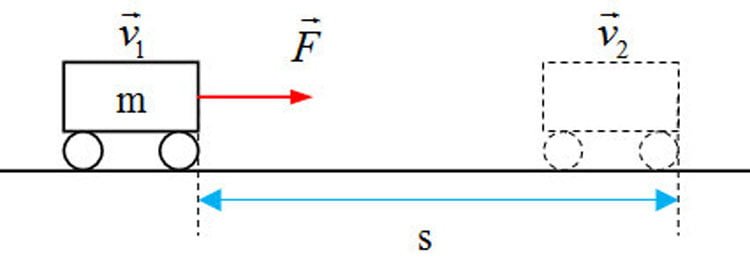
Công:
![]()
(Chỉ áp dụng cho trường hợp lực không thay đổi và quỹ đạo thẳng)
Công suất trung bình:
![]()
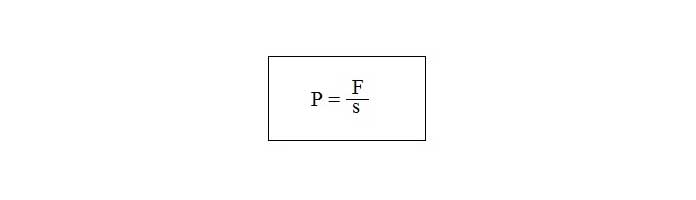
Công suất tức thời:
![]()
Động năng:
![]()
Liên hệ giữa động năng và công:
![]()
(Công của ngoại lực F)
Thế năng trọng trường:
![]()
Liên hệ giữa thế năng trọng trường và công:
![]()
Công của trọng lực(rơi):
![]()
(Khi vật đi lên thì thêm dấu “-“)
Thế năng đàn hồi:
![]()
Liên hệ giữa thế năng đàn hồi và công:
![]()
Cơ năng:
![]()
Định luật bảo toàn cơ năng:
![]()
(Cơ năng chỉ bảo toàn khi không có ngoại lực khống chế)
Độ cao động năng bằng n lần thế năng:
![]()
(Nếu thế năng bằng m lần động năng thì thay n=1/m , chỉ áp dụng khi làm bài trắc nghiệm hoặc kiểm tra kết quả)
Hiệu suất:
![]()
Aci: Công có ích
Atp: Công toàn phần
Bài tập minh họa định luật bảo toàn năng lượng
Một vật có m = 10g, rơi tự do tại độ cao 5m, vận tốc rơi 13km/h. Tìm cơ năng biết g= 9.8m/s2.
Lời giải:
Áp dụng công thức
![]()
Sotayhoctap chúc các bạn học tốt!