Bài viết khoảng cách từ điểm đến mặt phẳng bao gồm: khoảng cách từ 1 điểm đến 1 mặt phẳng, tính khoảng cách từ điểm đến mặt phẳng, khoảng cách từ điểm đến mặt phẳng oxyz, công thức khoảng cách từ điểm đến mặt phẳng…
Định nghĩa hhoảng cách từ điểm đến mặt phẳng
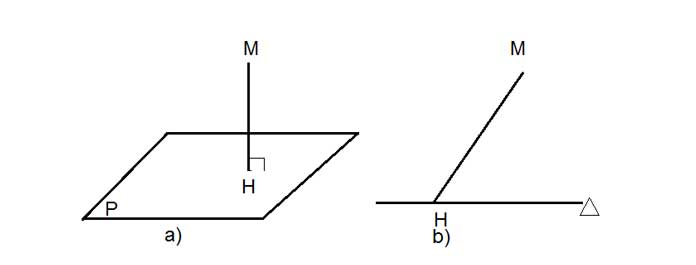
Khoảng cách từ 1 điểm M đến một mặt phẳng (P) (hoặc đến đường thẳng ∆) là khoảng cách giữa hai điểm M và H, trong đó H là hình chiếu của điểm M trên mặt phẳng (P) (h.a), kí hiệu là d(M, (P)) (hoặc trên đường thẳng ∆, kí hiệu là d(M, ∆) (h.b)).
Công thức hhoảng cách từ điểm đến mặt phẳng
Cho điểm M(a, b, c) và mặt phẳng (P): Ax + By + Cz + D = 0.
Khi đó khoảng cách từ điểm M tới (P) được xác định như sau:
![]()
Phương pháp xác định khoảng cách từ điểm đến mặt phẳng
Để xác định khoảng cách từ điểm ![]() đến mặt phẳng
đến mặt phẳng ![]() , ta sử dụng các phương pháp sau đây:
, ta sử dụng các phương pháp sau đây:
Phương pháp 1
+ Tìm mặt phẳng ![]() chứa
chứa ![]() và vuông góc với mặt phẳng
và vuông góc với mặt phẳng ![]() theo giao tuyến
theo giao tuyến ![]()
+ Từ ![]() hạ
hạ ![]() vuông góc với
vuông góc với ![]() (
(![]() ).
).
+ Khi đó ![]()
Ví dụ 1: Cho hình chóp đều ![]() , đáy
, đáy ![]() có cạnh bằng
có cạnh bằng ![]() , mặt bên tạo với đáy một góc
, mặt bên tạo với đáy một góc ![]() . Tính
. Tính ![]() theo
theo ![]() và
và ![]()
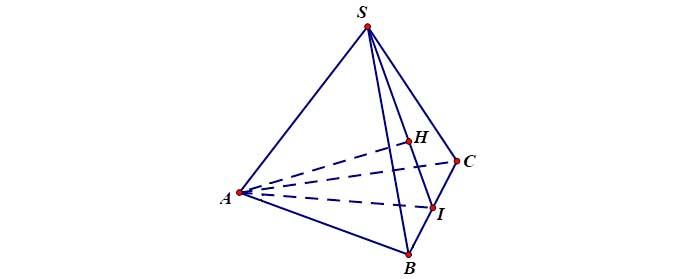
Gọi ![]() là trung điểm của
là trung điểm của ![]()
+ Ta có: ![]() và
và ![]()
+ Kẻ ![]() mà
mà ![]() nên
nên ![]() . Do đó,
. Do đó, ![]()
+ Mặt khác, xét tam giác vuông ![]() có:
có: ![]()
Vậy: ![]()
Ví dụ 2: Cho hình chóp ![]() đáy
đáy ![]() là hình vuông cạnh
là hình vuông cạnh ![]() ,
, ![]() ,
, ![]()
a) Tính ![]() .
.
b) Tính ![]() .
.
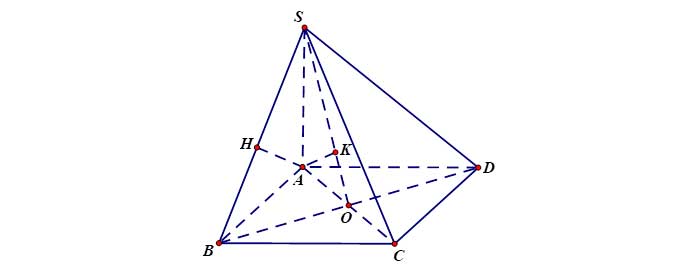
a) Kẻ ![]()
Ta có: ![]() và
và ![]() . Từ
. Từ ![]() và
và ![]() suy ra:
suy ra: ![]()
Từ ![]() và
và ![]() ta có:
ta có: ![]() hay
hay ![]()
+ Mặt khác, xét tam giác vuông ![]() có:
có: ![]()
![]()
Vậy ![]()
b) Gọi ![]()
Kẻ ![]()
Ta có: ![]() và
và ![]() . Từ
. Từ ![]() và
và ![]() suy ra:
suy ra: ![]()
Từ ![]() và
và ![]() ta có:
ta có: ![]() hay
hay ![]()
+ Mặt khác, xét tam giác vuông ![]() có:
có: ![]()
![]()
Vậy ![]()
Ví dụ 3: Cho hình chóp ![]() đáy
đáy ![]() là hình vuông cạnh
là hình vuông cạnh ![]() , tam giác
, tam giác ![]() đều,
đều, ![]() . Gọi
. Gọi ![]() lần lượt là trung điểm của
lần lượt là trung điểm của ![]() và
và ![]() . Tính
. Tính ![]()
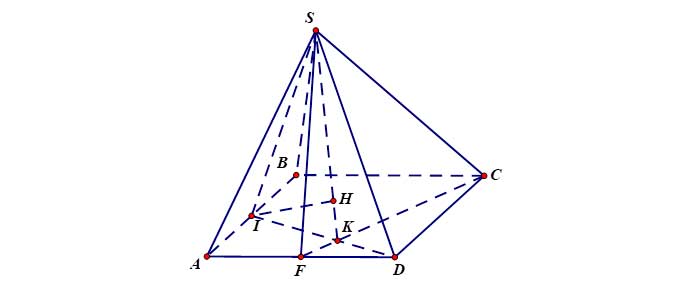
Gọi ![]()
+ Kẻ ![]()
+ Ta có:
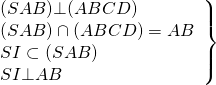
![]()
![]()
+ Mặt khác, xét hai tam giác vuông ![]() và
và ![]() có:
có: ![]() ,
, ![]()
Suy ra ![]()
![]()
Mà ![]()
![]()
Hay ![]()
![]()
+ Từ ![]() và
và ![]() ta có:
ta có: ![]()
![]() . Từ
. Từ ![]() và
và ![]() suy ra:
suy ra: ![]() hay
hay ![]()
+ Ta có:
![]()
![]()
![]()
![]()
Do đó ![]()
![]()
Vậy ![]()
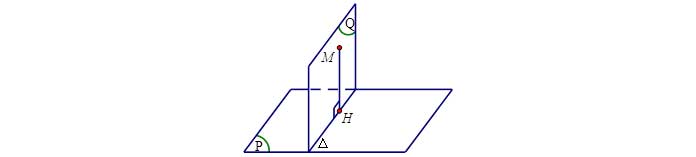
Phương pháp 2
+ Qua ![]() , kẻ
, kẻ ![]() . Ta có:
. Ta có: ![]()
+ Chọn ![]() . Lúc đó
. Lúc đó ![]() .
.

Ví dụ 4: Cho lăng trụ ![]() ,
, ![]() là hình chữ nhật,
là hình chữ nhật, ![]() . Hình chiếu vuông góc của
. Hình chiếu vuông góc của ![]() trên
trên ![]() trùng với giao điểm của
trùng với giao điểm của ![]() và
và ![]() . Tính
. Tính ![]()
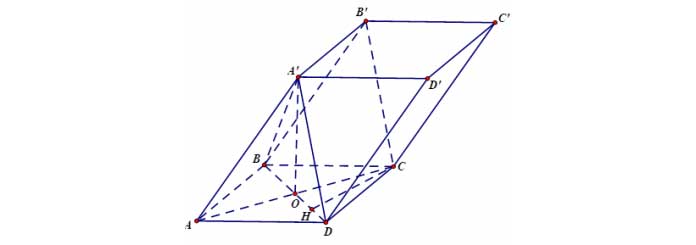
+ Gọi ![]() là giao điểm của
là giao điểm của ![]() và
và ![]() Vì
Vì ![]() nên
nên ![]() . Do đó:
. Do đó: ![]()
![]()
+ Trong mặt phẳng ![]() kẻ
kẻ ![]() . Mặt khác
. Mặt khác ![]()
![]()
Từ ![]() và
và ![]() suy ra:
suy ra: ![]()
![]()
+ Xét tam giác vuông ![]() có:
có: ![]()
![]()
Vậy: ![]()
Ví dụ 5: Cho hình chóp ![]() có đáy
có đáy ![]() là tam giác vuông tại
là tam giác vuông tại ![]() ,
, ![]() ,
, ![]() là tam giác đều cạnh
là tam giác đều cạnh ![]() ,
, ![]() . Tính
. Tính ![]() .
.
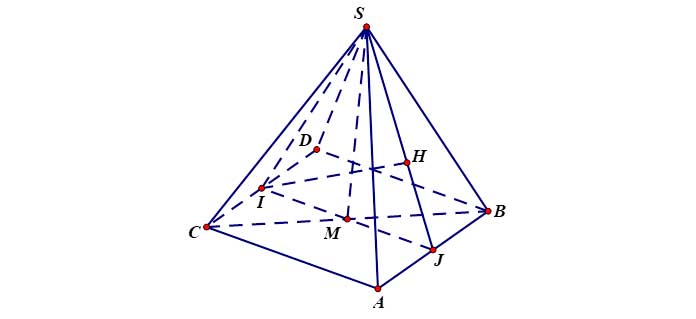
+ Trong mặt phẳng ![]() vẽ hình chữ nhật
vẽ hình chữ nhật ![]() . Gọi
. Gọi ![]() lần lượt là trung điểm của
lần lượt là trung điểm của ![]() và
và ![]() . Lúc đó,
. Lúc đó, ![]() hay:
hay: ![]()
![]()
+ Trong mặt phẳng ![]() kẻ
kẻ ![]()
Mặt khác, ta có: ![]()
![]()
Từ ![]() và
và ![]() suy ra:
suy ra: ![]() hay
hay ![]()
+ Xét tam giác ![]() có:
có: ![]()
![]()
Với: ![]() ,
, ![]() ,
, ![]() .
.
Do đó: ![]()
Vậy ![]()
Phương pháp 3
+ Nếu ![]() . Ta có:
. Ta có: ![]() .
.
+ Tính ![]() và
và ![]() .
.
+ ![]() .
.
Chú ý: Điểm ![]() ở đây ta phải chọn sao cho tìm khoảng cách từ
ở đây ta phải chọn sao cho tìm khoảng cách từ ![]() đến mặt phẳng
đến mặt phẳng ![]() dễ hơn tìm khoảng cách từ
dễ hơn tìm khoảng cách từ ![]() đến mặt phẳng
đến mặt phẳng ![]()

Ví dụ 6: Cho hình chóp ![]() có đáy
có đáy ![]() là hình thang vuông tại
là hình thang vuông tại ![]() và
và ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
a) Tính ![]()
b) Tính ![]()
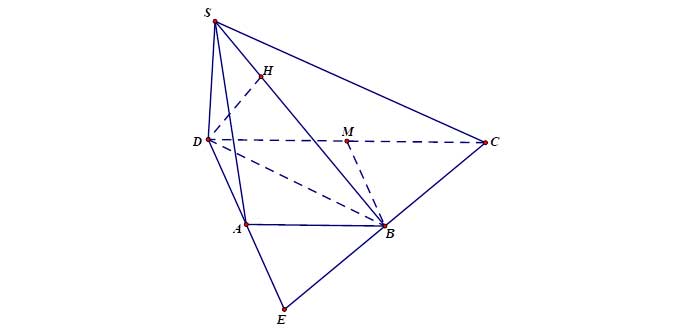
Gọi ![]() là trung điểm của
là trung điểm của ![]() ,
, ![]() là giao điểm của hai đường thẳng
là giao điểm của hai đường thẳng ![]() và
và ![]()
a) Trong mặt phẳng ![]() kẻ
kẻ ![]()
+ Vì ![]() Tam giác
Tam giác ![]() vuông tại
vuông tại ![]() hay
hay ![]() . Mặt khác, vì
. Mặt khác, vì ![]()
Từ ![]() và
và ![]() ta có:
ta có:
![]()
Từ ![]() và
và ![]() suy ra:
suy ra: ![]() hay
hay ![]()
+ Xét tam giác vuông ![]() có:
có: ![]()
![]()
Vậy ![]()
b) Ta có: ![]()
![]()
![]()
Vậy ![]()
Ví dụ 7: Cho hình chóp ![]() có đáy
có đáy ![]() là tam giác vuông tại
là tam giác vuông tại ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Tính
. Tính ![]() .
.
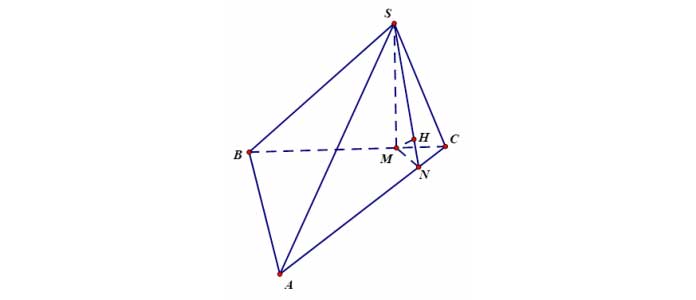
+ Trong mặt phẳng ![]() kẻ
kẻ ![]() ; trong mặt phẳng
; trong mặt phẳng ![]() kẻ
kẻ ![]() ; trong mặt phẳng
; trong mặt phẳng ![]() kẻ
kẻ ![]() . Suy ra,
. Suy ra, ![]()
![]()
+ Ta có: ![]()
![]()
![]()
![]() . Xét tam giác vuông
. Xét tam giác vuông ![]() có:
có: ![]()
![]()
![]()
+ Mặt khác, ta có:
![]()
![]()
![]()
Vậy ![]()
Sotayhoctap chúc các bạn học tốt!