Bài viết các quy tắc tính đạo hàm sẽ giới thiệu đến các em công thức tính đạo hàm của các hàm số thường gặp và hàm hợp của chúng, các quy tắc tính đạo hàm của tổng, hiệu, tích, thương. Bên cạnh đó là những ví dụ minh họa có hướng dẫn giải chi tiết sẽ giúp các em hình thành và rèn luyện kĩ năng tính đạo hàm.

Quy tắc tính đạo hàm
Đạo hàm của một số hàm số thường gặp
Định lý 1: Hàm số ![]() ) có đạo hàm với mọi
) có đạo hàm với mọi ![]() và:
và: ![]()
Nhận xét:
(c)’=0 (với c là hằng số).
(x)’=1.
Định lý 2: Hàm số ![]() có đạo hàm với mọi x dương và:
có đạo hàm với mọi x dương và: ![]()
Đạo hàm của tổng, hiệu, tích, thương
Định lý 3: Giả sử ![]() và
và ![]() là các hàm số có đạo hàm tại điểm x thuộc khoảng xác định. Ta có:
là các hàm số có đạo hàm tại điểm x thuộc khoảng xác định. Ta có:
![]()
![]()
![]()
![]()
Mở rộng:
![]()
Hệ quả 1: Nếu k là một hằng số thì: ![]()
Hệ quả 2: ![]() ,
, ![]()
![]()
Đạo hàm với hàm hợp
Định lý: Cho hàm số ![]() với
với ![]() thì ta có:
thì ta có: ![]()
Hệ quả:
![]()
![]()
Download bảng công thức đạo hàm đầy đủ pdf
Các bạn có thể tải bảng công thức đạo hàm đầy đủ pdf dưới đây để in ra tiện cho việc tra cứu và học tập.
Ví dụ cho các quy tắc tính đạo hàm
Ví dụ 1:
a) Cho hàm số f(x)=x6. Tính f'(x) và f'(1).
b) Tính đạo hàm của hàm số ![]() tại x=9.
tại x=9.
Hướng dẫn giải:
a) Ta có: ![]()
Vậy: ![]()
b) Ta có: ![]()
Tại x=9 ta có: ![]()
Ví dụ 2:
Tính đạo hàm của các hàm số sau:
a) ![]()
b) ![]()
c) ![]()
Hướng dẫn giải:
a) ![]()
b) ![]()
![]()
c) ![]()
Ví dụ 3:
Tính đạo hàm của các hàm số sau:
a) ![]()
b) ![]()
c) ![]()
Hướng dẫn giải:
a) ![]()
b) ![]()
c) ![]()
![]()
Ví dụ 4:
Tính đạo hàm của các hàm số sau:
a) ![]()
b) ![]()
c) ![]() với a là hằng số.
với a là hằng số.
Hướng dẫn giải:
a) ![]()
b) ![]()
![]()
c) ![]()
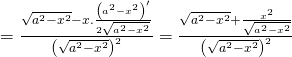
![]()




