
Cashback là gì? Có nên sử dụng cashback hay không?
Ngày nay, nhu cầu mua sắm và thanh toán qua thẻ của con người ngày càng cao. Với mục đích phục vụ tốt trải nghiệm của người…

[Hướng Dẫn] Sử Dụng Tủ Gửi Đồ Thông Minh Đơn Giản Nhất
Xã hội ngày càng phát triển, kéo theo đó là các công nghệ hiện đại được sáng tạo không ngừng nghỉ. Một trong những sáng tạo tiện…
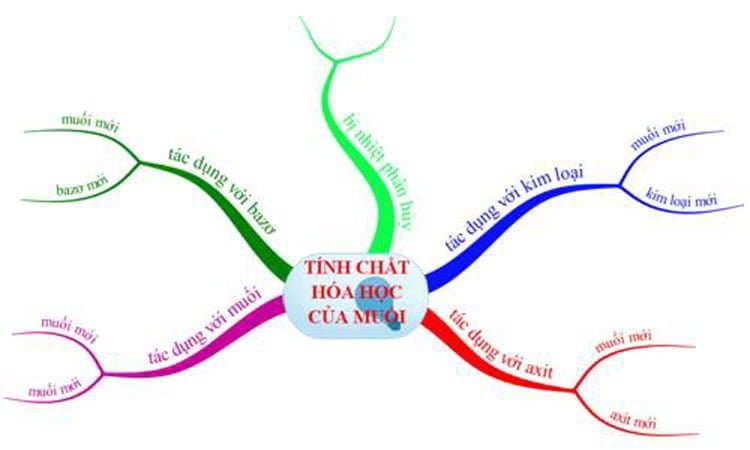
Tính chất hóa học của muối và điều kiện
Bài viết tính chất hóa học của muối bao gồm: tính chất hóa học của muối và điều kiện, phản ứng trao đổi trong dung dịch, ví…
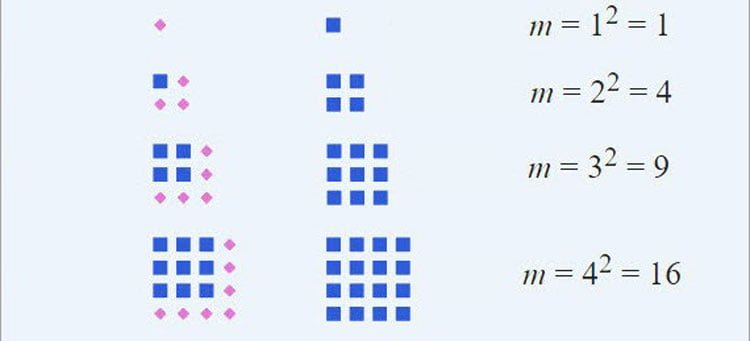
Chuyên đề số chính phương
Chuyên đề số chính phương: số chính phương là số gì, định nghĩa số chính phương, tính chất số chính phương, một số dạng bài tập về…
Lược đồ Hoocne (Sơ đồ Hoocne) trong cách chia đa thức
Bài viết lược đồ Hoocne (Sơ đồ Hoocne) trong cách chia đa thức bao gồm: Cách chia đa thức cho đa thức bằng lược đồ Hoocne, bài…
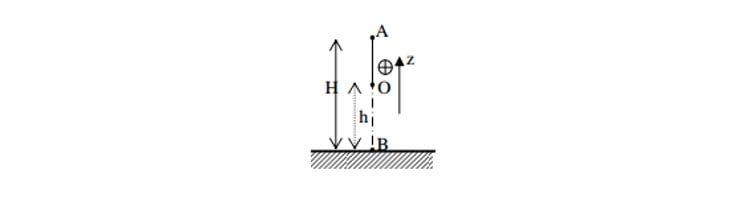
Định luật bảo toàn cơ năng và phương pháp giải
Bài viết định luật bảo toàn cơ năng bao gồm: định luật bảo toàn cơ năng, phương pháp giải bài toán về định luật bảo toàn cơ…
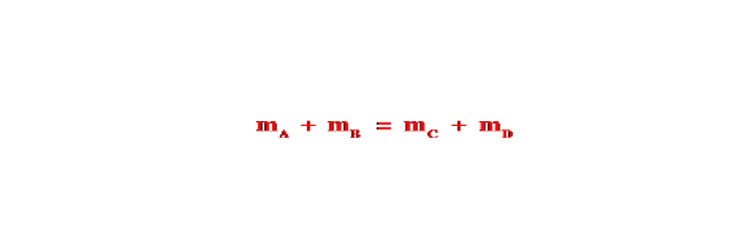
Định luật bảo toàn khối lượng – Phương pháp áp dụng
Bài viết định luật bảo toàn khối lượng bao gồm: định luật bảo toàn khối lượng là gì, cách áp dụng định luật bảo toàn khối lượng,…
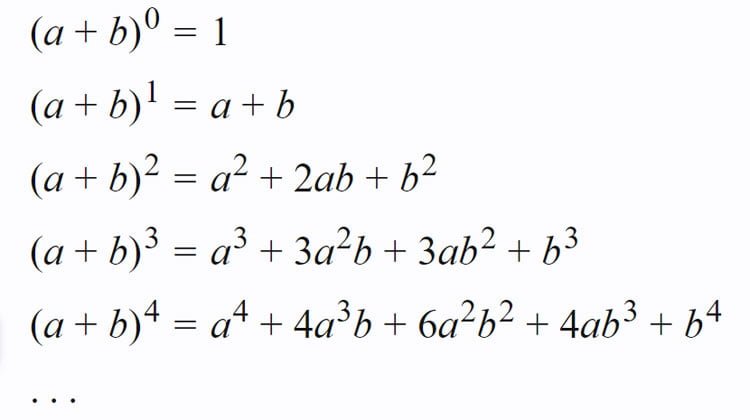
Nhị thức Newton, cách khai triển và một số dạng bài tập áp dụng
Bài viết nhị thức Newton bao gồm: nhị thức Newton cơ bản, khai triển nhị thức Newton, tìm hệ số trong khai triển nhị thức Newton, nhị…

Những hằng đẳng thức đáng nhớ, hằng đẳng thức mở rộng và dạng toán áp dụng
Bài viết những hằng đẳng thức đáng nhớ bao gồm: 7 hằng đẳng thức đáng nhớ, các hằng đẳng thức mở rộng, các hằng đẳng thức tổng…
Hằng số Avogadro, câu hỏi và bài tập áp dụng
Bài viết hằng số Avogadro bao gồm: số Avogadro là gì, số Avogadro bằng bao nhiêu, số Avogadro cho biết điều gì… Số Avogadro là gì? Ðịnh…